Предположим, что ставится задача не только построить модель зависимости цены p квартиры от факторов x 1, x 2, …, xm, но и решить вопрос существенности (или несущественности) влияния фактора: «квартира в панельном или кирпичном доме». Другими словами, необходимо выяснить, можно ли считать одним и тем же уравнение регрессии 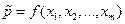 для панельных и кирпичных домов или необходимо всю имеющуюся выборку разбить на две части (одну для панельных домов, а другую для кирпичных) и построить для каждой из них свое уравнение регрессии.
для панельных и кирпичных домов или необходимо всю имеющуюся выборку разбить на две части (одну для панельных домов, а другую для кирпичных) и построить для каждой из них свое уравнение регрессии.
Формальный статистический тест для оценки объединенной регрессии в сравнении с регрессиями для подвыборок был предложен Грегори Чоу. Суть теста Чоу в следующем:
1) полная выборка объема n разбивается на две подвыборки А и В объемами n 1 и n 2 соответственно (n = n 1 + n 2);
2) для полной выборки, а также для подвыборок А и В оцениваются параметры линейных уравнений регрессии:
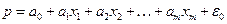 , (0)
, (0)
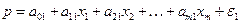 , (1)
, (1)
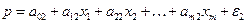 ; (2)
; (2)
3) выдвигается и проверяется гипотеза о равенстве друг другу соответствующих коэффициентов регрессии, а именно гипотеза 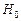 :
: 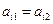 ,
, 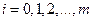 , с помощью F -статистики
, с помощью F -статистики 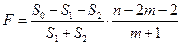 , где
, где 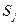 – сумма квадратов отклонений выборочных значений
– сумма квадратов отклонений выборочных значений 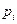 от соответствующих значений цены, рассчитанных по уравнению регрессии (j),
от соответствующих значений цены, рассчитанных по уравнению регрессии (j), 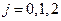 ,
, 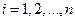 ,
, 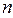 – объем выборки.
– объем выборки.
Построенная F -статистика имеет распределение Фишера с числами степеней свободы 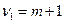 и
и 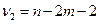 . Если F > F кр, то гипотеза
. Если F > F кр, то гипотеза 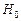 отклоняется. В этом случае моделирование следует осуществлять с помощью кусочно-линейной модели. Если же F < F кр, то нет оснований отклонить нулевую гипотезу, а значит, ее моделирование следует осуществлять с помощью единого для всей совокупности уравнения.
отклоняется. В этом случае моделирование следует осуществлять с помощью кусочно-линейной модели. Если же F < F кр, то нет оснований отклонить нулевую гипотезу, а значит, ее моделирование следует осуществлять с помощью единого для всей совокупности уравнения.
Геометрическая интерпретация выводов тестирования в случае парной линейной динамической модели заключается в следующем. Если F < F кр, то по заданному корреляционному полю единая прямая хорошо моделирует ситуацию. Если же F > F кр, то по тому же корреляционному полю следует отдать предпочтение моделированию некоторой ломаной линией.
 2015-04-17
2015-04-17 365
365








