Примеры решения заданий. Пример 1.В игре принимают участие два игрока

Пример 1. В игре принимают участие два игрока. Каждый из игроков может записать независимо от другого цифру 4, 5 или 6. Если разность между цифрами, записанными игроками А и В положительна, то игрок А выигрывает количество очков, равное этой разности. Если разность отрицательна, то выигрывает игрок В. Если разность равна нулю, то игра заканчивается вничью. Составить платежную матрицу и найти решение игры.

Решение:

Составим платежную матрицу игры. Чистыми стратегиями игрока А будут: А 1 – записать число 4; А 2 – записать число 5; А 3 – записать число 6. У игрока В чистыми будут аналогичные стратегии. Элемент матрицы а ₁₁ = 0, так как в ситуации (А 1; В 1) оба игрока записывают цифру 4 и выигрыш игрока А равен 4 – 4 = 0. В ситуации (А1; В 2) выигрыш игрока А составит а ₁₂ = 4–5 = –1. Аналогичным образом вычисляются остальные элементы платежной матрицы (рисунок 1).

	B 1 (4)	B 2 (5)	B 3 (6)	a i
A 1(4)		–1	–2	–2
A2 (5)			–1	–1
A3(6)			0*
b j

Рисунок 1. Платежная матрица примера

Определим минимальные гарантированные выигрыши игрока А, равные 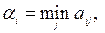при выборе им стратегий А _i. Так, если игрок А записал цифру 4, то его минимальный выигрыш при выборе данной стратегии составит a₁ = min(0; –1; –2) = –2. Аналогично находим a₂ = min(1; 0; –1)= –1, если игрок А записал цифру 5 и a₃ = min(2; 1; 0) = 0, если им записана цифра 6. Найдем нижнюю цену игры игрока А, воспользовавшись “принципом максимина”, т. е. 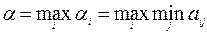. Нижняя цена игры для игрока А составит a = max(–2; –1; 0) = 0. Таким образом, максиминному выбору игрока А будет отвечать третья стратегия, гарантирующая выигрыш, равный нулю.

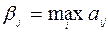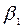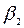Для игрока В значения элементов составят соответственно = 2, = 1, 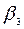= 0. Верхняя чистая цена игры для игрока В по “принципу минимакса” составит 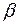= min (2; 1; 0) = 0. Следовательно, минимаксному выбору игрока В будет отвечать третья стратегия, гарантирующая минимальный проигрыш, равный нулю.

Так как a = b, то данная игра имеет седловую точку, т. е. третья чистая стратегия игрока А и третья чистая стратегия игрока В образуют седловую точку со значением 0 и данная матричная игра имеет решение (A ₃; B ₃; 0).

Пример 2. Выполнить возможные упрощения платежной матрицы:

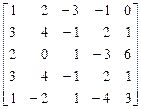. (1)

Решение:

Поскольку соответствующие элементы второй и четвертой строк матрицы (1) равны, то имеет место случай с дублирующими стратегиями. Следовательно, одну из строк можно убрать (например, четвертую). Элементы первой строки меньше соответствующих элементов второй строки, а элементы пятой строки меньше или равны соответствующим элементам третьей строки. Поэтому игроку А, стремящемуся максимизировать выигрыш, выгоднее применять стратегии А ₂ и А ₃, а не стратегии А ₁ и А ₅. В связи с этим опустим первую и пятую строки, получим платежную матрицу 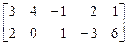(2):

. (2)

В преобразованной матрице (2) элементы первого и второго столбцов больше соответствующих элементов четвертого столбца. Поэтому игроку B, стремящемуся минимизировать проигрыш, стратегии В₁ и В ₂ являются заведомо невыгодными. В связи с этим опустим первый и второй столбцы. По аналогичной причине после сравнения пятого и третьего столбцов опускаем пятый столбец. В результате приходим к матрице 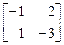(3):

. (3)

Далее, для того, чтобы перевести элементы матрицы (3) в область неотрицательных значений добавим к каждому из них число 4. Получим матрицу 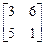(4):

. (4)

Сравнивая вновь строки полученной матрицы, заключаем, что дальнейшему упрощению она не подлежит.

Пример 3. Туристическая фирма реализует туристические путевки. Объем реализации путевок изменяется в зависимости от потребительского спроса в пределах от 6 до 9 ед. Если путевок меньше, чем требует спрос на них, то фирма может заказать недостающее количество. При этом возникнут дополнительные расходы в размере 5 усл. ед. за каждую новую путевку. А если количество путевок превышает спрос, то потери за невостребованную путевку составят 6 усл. ед. Прибыль от реализации одной путевки составляет 10 усл. ед.

Требуется определить, какое количество путевок выгоднее брать на реализацию.

Решение:

В данном примере первым игроком является руководство туристической фирмы, которое может принять одно из решений:

а) А 1 – заказать 6 путевок;

б) А 2 – заказать 7 путевок;

в) А 3 – заказать 8 путевок;

г) А 4 – заказать 9 путевок.

Потребительский спрос выступает в качестве второго игрока, “природы”, стратегии которой определяются данными спроса, т. е.:

а) стратегия П 1 – “купят 6 путевок”;

б) стратегия П 2 – “купят 7 путевок”;

в) стратегия П 3 – “купят 8 путевок”;

г) стратегия П 4 – “купят 9 путевок”.

Построим платежную матрицу игры (рисунок 2).

	П 1 = 6	П 2 = 7	П 3 = 8	П 4 = 9
А1 = 6
А 2 = 7
А 3 = 8
А 4 = 9

Рисунок 2. Платежная матрица

Рассчитаем элементы а_ij платежной матрицы игры.

Выигрыш игрока А (руководства фирмы), если он заказал 6 путевок (А 1 = 6), а спрос оказался равным также 6 (П 1 = 6) будет равен:

а ₁₁ = 6 × 10 = 60 усл. ед.,

где 6 × 10 – прибыль от реализации шести путевок.

Выигрыш игрока А, когда заказано А 1 = 6 путевок, а спрос П 2 = 7 путевок:

а ₁₂ = 7 × 10 – 1 × 5 = 70 – 5 = 65 усл. ед.,

где 7 × 10 – прибыль от реализации семи путевок; 1 × 5 – затраты, связанные с заказом дополнительной путевки.

Аналогично рассчитаем элемент а ₁₃, когда заказано А 1 = 6 путевок, а спрос составил П 3=8 путевок:

а ₁₃ = 8 × 10 – 2 × 5 = 80 – 10 = 70 усл. ед.,

где 8 × 10 – прибыль от реализации восьми путевок; 2 × 5 – затраты, связанные с заказом двух дополнительных путевок.

Когда заказано А 1 = 6 путевок, а спрос П 4 = 9 путевок, выигрыш игрока А:

а ₁₄ = 9 × 10 – 3 × 5 = 90 – 15 = 75 усл. ед.

Рассчитаем элемент а ₂₁, когда заказано А 2 = 7 путевок, а спрос составил П 1 = 6 путевок:

а ₂₁ = 6 × 10 – 1 × 6 = 60 – 6 = 54 усл. ед,

где 6 × 10 – прибыль от реализации шести путевок; 1 × 6 – потери за одну невостребованную путевку.

Остальные элементы платежной матрицы вычисляются аналогично:

а ₂₂ = 7 × 10 = 70 усл. ед.;

а ₂₃ = 8 × 10 – 1 × 5 = 80 – 5 = 75 усл. ед.;

а ₂₄ = 9 × 10 – 2 × 5 = 90 – 10 = 80 усл. ед.;

а ₃₁ =6 × 10 – 2 × 6 = 60 – 12 = 48 усл. ед.;

а ₃₂ =7 × 10 – 1 × 6 = 70 – 6 = 64 усл. ед.;

а ₃₃ = 8 × 10 = 80 усл. ед.;

а ₃₄ = 9 × 10 – 1 × 5 = 90 – 5 = 85 усл. ед.;

а ₄₁ =6 × 10 – 3 × 6 = 60 – 18 = 42 усл. ед.;

а ₄₂ =7 × 10 – 2 × 6 = 70 – 12 = 58 усл. ед.;

а ₄₃ = 8 × 10 – 1 × 6 = 80 – 6 = 74 усл. ед.; а ₄₄ =9 × 10 = 90 усл. ед.

Так как вероятности состояния спроса заранее нам не известны, использовать критерии Байеса и Лапласа невозможно. Найдем решение игры по критериям Вальда, Сэвиджа и Гурвица (l = 0,7).