Пусть в многоканальную СМО (n > 1) поступает пуассоновский поток требований с интенсивностью l. Интенсивность обслуживания заявок равна m. Если канал занят, то заявка поступает в очередь, число мест в которой неограничено (m = ¥ ).
Прежде чем приступить к расчету основных характеристик такой СМО, необходимо проверить выполнение условия ее работоспособности, т.е. a < n. Если это условие нарушается, то очередь заявок будет неограниченно расти, и система не справится с их обслуживанием.
Формулы для расчета основных характеристик работы многоканальной СМО с ожиданием и неограниченной очередью приведены в таблице 7.
Таблица 14. Основные характеристики работы многоканальной
СМО с ожиданием и неограниченной очередью
| Наименование показателя | Формула расчета |
| Вероятность того, что система свободна | 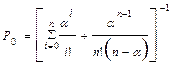 |
| Вероятность того, что все каналы заняты, но очереди еще нет | 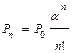 |
| Вероятность того, что в очереди находится r требований | 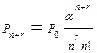 |
| Вероятность отказа в обслуживании | 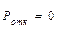 |
| Относительная пропускная способность | Q = 1 – Pотк = 1 (таким образом, заявка всегда обслуживается) |
| Абсолютная пропускная способность | A =l Q = l (т. е. выходной поток требований совпадает со входным) |
| Среднее число каналов, занятых обслуживанием заявок | 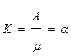 |
| Средняя длина очереди | 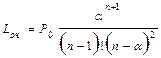 |
| Среднее число заявок, находящихся в системе | Lсис = Lоч + K |
| Среднее время ожидания заявки в очереди | 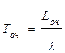 |
| Среднее время пребывания заявки в системе | 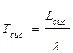 |
 2015-04-17
2015-04-17 1035
1035








