Теорема 6. Если все элементы сходящейся последовательности  ,
, 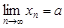 , начиная с некоторого номера, удовлетворяют неравенству
, начиная с некоторого номера, удовлетворяют неравенству 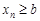 (
(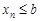 ), то и предел этой последовательности удовлетворяет неравенству
), то и предел этой последовательности удовлетворяет неравенству 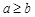 (
(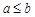 ).
).
► Доказываем методом от противного. Предположим, что выполняется неравенство 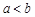 .
.
По определению предела
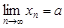
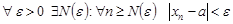 .
.
Положим 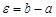 . Тогда
. Тогда 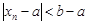 . После несложных преобразований получим
. После несложных преобразований получим 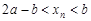 . Из правой части этого неравенства
. Из правой части этого неравенства 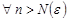 имеем
имеем 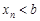 . Это противоречит условию, что
. Это противоречит условию, что 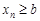 . Значит, справедливо неравенство
. Значит, справедливо неравенство 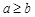 .
.
Аналогично доказывается случай 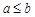 . ◄
. ◄
Теорема 7 (о промежуточной переменной). Пусть последовательности  ,
, 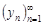 ,
, 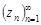 таковы, что:
таковы, что:
1) 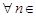
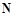 выполняется неравенство
выполняется неравенство 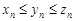 ,
,
2) 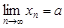 ,
, 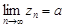 .
.
Тогда последовательность 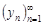 сходится и
сходится и 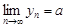 .
.
► По определению предела имеем
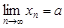
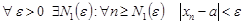 .
.
Из последнего неравенства 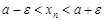 .
.
Аналогично
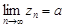
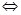
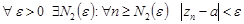 .
.
Отсюда 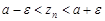 .
.
Возьмем 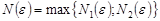 . Тогда для всех
. Тогда для всех 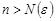 выполняются неравенства одновременно
выполняются неравенства одновременно
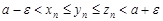 .
.
Отсюда 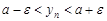 или
или 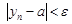 . Это означает, что
. Это означает, что 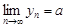 . ◄
. ◄
 2015-04-17
2015-04-17 716
716








