2015-04-17
3766
Пусть дана бесконечная последовательность комплексных чисел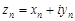 
, 
....
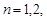Комплексное число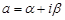 
, 
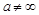, называется пределомчисловойпоследовательности 
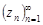, если для любого 
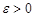существует номер 
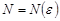такой, что для всякого 
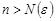справедливо неравенство 
.
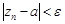Обозначается: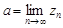 
.
Комплексное число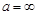 
называется пределом числовой последовательности 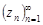, если 
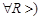найдется такой номер 
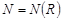, что для любого 
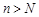выполняется неравенство 
.
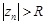Обозначается: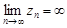 
.
Существование конечного предела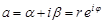 
последовательности комплексных чисел = 
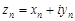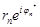, где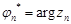 
, равносильно существованию как двух пределов вещественных последовательносте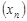й 
и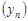 
, а при специальной оговорке относительно главных значений аргументов 
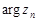, так и пределов последовательносте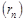й 
и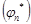 
.
Теорема 1. Для того чтобы существовал конечный предел последовательности , ,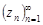
,
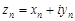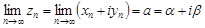необходимо и достаточно, чтобы существовали пределы последовательносте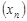й и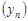
, 
.
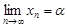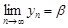► Необходимость. Пусть существует конечный предел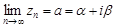 
. По определению предела
: .
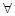
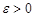
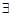
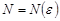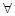
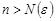
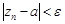Модуль комплексного числа равен
.
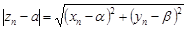Поэтому
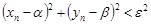при .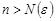
Отсюда следуют неравенства
|
|
|
, 
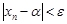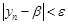при .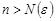
Это означает, что существуют пределы
, .
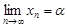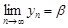Достаточность. Пусть существуют пределы
, .
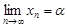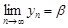По определению предела
: 
,
: 
.
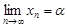
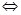
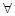
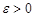
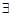
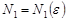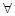
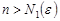
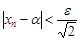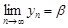
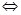
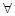
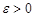
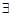
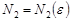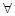
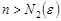
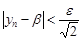Возьмем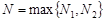 
. Тогда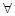 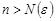выполняется неравенство
.
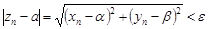Отсюда следует, что существует предел .◄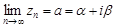
Теорема 2. Для того чтобы существовал конечный предел ,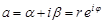 
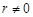, последовательности 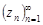, 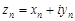= 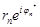, необходимо и достаточно, чтобы существовал предел 
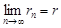, а при надлежащем выборе области главных значений аргументов 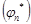и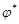 
предел 
.
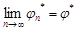Теорема 3 (критерий Коши). Для того чтобы последовательность 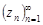комплексных чисел была сходящейся, необходимо и достаточно, чтобы для любого 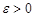существовал номер 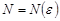такой, что для всякого 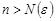и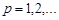 
справедливо неравенство 
.
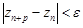Все действия с пределами последовательностей комплексных чисел аналогичны действиям с последовательностями действительных чисел.
Вопрос 2 Дифференцируемость функции одной и нескольких переменных в точке. Необходимое и достаточное условие дифференцируемости в точке функции одной и нескольких переменных. Связь между дифференцируемостью и непрерывностью функции в точке.
