Определение производной

Пусть функция 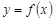определена в некоторой окрестност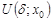и точки . Если фиксированное значение аргумента получает приращение 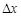(положительное или отрицательное), такое, что 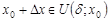, то приращение функции определяется выражением .

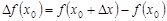Производной функции 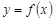в произвольной фиксированной точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю:

.

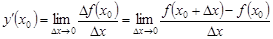Обозначается: , , , .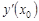

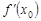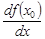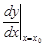Производная функции 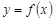в произвольной точке 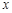обозначается так: , , , .

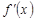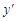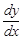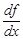Если для некоторого значения 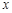предел 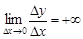или 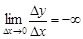, то говорят, что функция 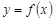в точке 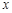имеет бесконечную производную.

Операция нахождения производной функции 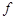называется дифференцированием.