Определение числового ряда, необходимый признак сходимости

Пусть 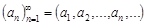– числовая последовательность. Выражение вида

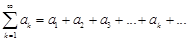
называется числовым рядом, числа 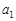, , 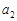…, , … 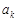– членами ряда, а число 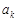– 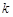-м или общим членом ряда.

Сумма конечного числа 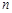первых членов

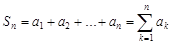
называется 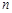-й частичной суммой данного ряда.

Если для последовательности 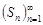частичных сумм ряда 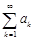существует конечный предел 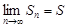, то ряд 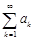называется сходящимся, а число 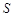– суммой данного ряда:

.

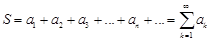Если предел последовательности 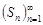не существует или равен бесконечности, то ряд называют расходящимся.

Теорема 1 (необходимое условие сходимости числового ряда) Если ряд 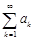сходится, то предел общего члена равен нулю: .

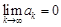Выражение вида 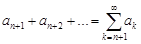, представляющее собой числовой ряд, называется 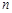- м остатком ряда 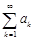и обозначается 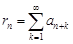или .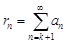

Для сходящегося ряда можно записать равенство

.

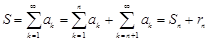Теорема 2 Для сходимости ряда 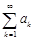необходимо и достаточно, чтобы любой его остаток 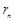сходился.

Очевидно, что если числовой ряд 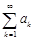сходится, т. е. 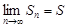, то

.

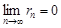Следовательно, отбрасывание любого конечного числа членов не влияет на сходимость ряда.