Теорема 1. Если функция 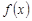 непрерывна на отрезке
непрерывна на отрезке 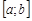 , то она интегрируема на этом отрезке, т.е. существует интеграл
, то она интегрируема на этом отрезке, т.е. существует интеграл 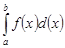 .
.
►Ограниченность 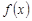 на отрезке
на отрезке 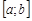 следует из теоремы Вейерштрасса.
следует из теоремы Вейерштрасса.
По теореме Кантора эта функция равномерно непрерывна на отрезке 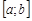 . Значит, для любого
. Значит, для любого 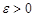 найдется такое
найдется такое 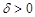 , что для любых
, что для любых 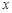 и
и 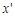 , принадлежащих отрезку
, принадлежащих отрезку 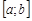 , из неравенства
, из неравенства 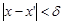 следует неравенство
следует неравенство 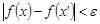 .
.
Возьмем такое разбиение 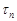 отрезка
отрезка 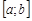 на частичные отрезки
на частичные отрезки 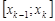 ,
, 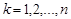 , чтобы
, чтобы 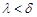 . Тогда
. Тогда 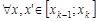 из неравенства
из неравенства 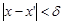 выполняется неравенство
выполняется неравенство
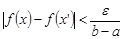 .
.
Отсюда следует, что 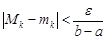 .С учетом этого
.С учетом этого
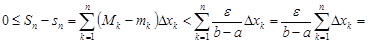
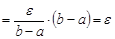 .
.
Значит, 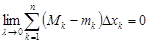 и
и 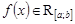 ◄
◄
Следствие 1. Если функция 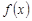 ограничена на отрезке
ограничена на отрезке 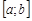 и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
и непрерывна на нем всюду, кроме конечного числа точек разрыва первого рода, то она интегрируема на этом отрезке.
Теорема 2. Функция 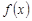 , монотонная на отрезке
, монотонная на отрезке 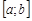 , то интегрируема на этом отрезке.
, то интегрируема на этом отрезке.
► Ограниченность 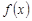 на отрезке
на отрезке 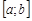 следует из свойств непрерывных функций.
следует из свойств непрерывных функций.
Пусть 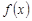 возрастает на отрезке
возрастает на отрезке 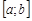 , т.е.
, т.е. 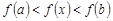 . Пусть
. Пусть 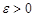 . Возьмем такое разбиение
. Возьмем такое разбиение 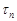 отрезка
отрезка 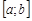 на частичные отрезки
на частичные отрезки 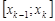 ,
, 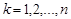 , чтобы
, чтобы
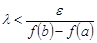 .
.
В силу монотонности 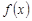 имеем
имеем
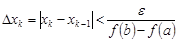 и
и 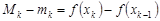 .
.
Тогда
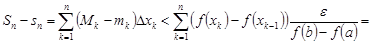
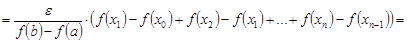
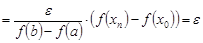 .
.
Следовательно, 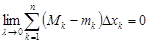 . В силу критерия Дарбу
. В силу критерия Дарбу 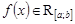 ◄
◄
3.4. Основные свойства определенного интеграла. О пределенный интеграл обладает следующими свойствами.
1. Если нижний и верхний пределы интегрирования равны 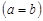 , то интеграл равен нулю:
, то интеграл равен нулю: 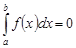 .Это свойство следует из определения интеграла.
.Это свойство следует из определения интеграла.
2. Если 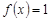 , то
, то 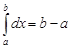 .
.
►Действительно, так как 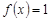 , то
, то 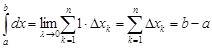 . ◄
. ◄
3. При перестановке пределов интегрирования определенный интеграл меняет знак на противоположный:
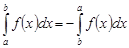 .
.
► Данное утверждение следует из того, что в случае 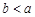 все числа
все числа 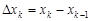 в разбиении
в разбиении 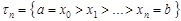 будут отрицательными (при
будут отрицательными (при 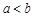 все
все 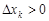 ). ◄
). ◄
Интеграл 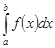 был определен для случая
был определен для случая 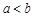 . Если
. Если 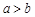 , свойство 3 рассматривается как дополнение к определению определенного интеграла. Его можно интерпретировать следующим образом: определенные интегралы
, свойство 3 рассматривается как дополнение к определению определенного интеграла. Его можно интерпретировать следующим образом: определенные интегралы 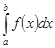 и
и 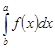 являются пределами интегральных сумм, различающихся лишь знаком.
являются пределами интегральных сумм, различающихся лишь знаком.
4. Постоянный множитель можно выносить за знак определенного интеграла:
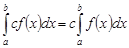
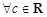 .
.
► Действительно,
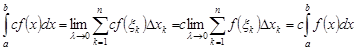 . ◄
. ◄
5. Определенный интеграл от алгебраической суммы конечного числа интегрируемых на 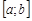 функций
функций 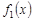 ,
, 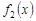 , …,
, …, 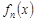 равен алгебраической сумме определенных интегралов от слагаемых:
равен алгебраической сумме определенных интегралов от слагаемых:
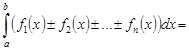
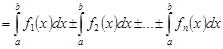 .
.
Доказательство этого свойства аналогично приведенному выше.
Замечание. Совокупность свойств 4 и 5 называются свойством линейности: если 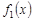 и
и 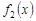 интегрируемы на
интегрируемы на 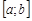 , то любая их линейная комбинация
, то любая их линейная комбинация 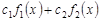 ,
, 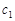 ,
, 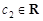 , также интегрируема на
, также интегрируема на 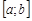 :
:
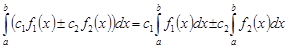 .
.
6 (аддитивность). Если существуют интегралы 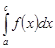 и
и 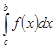 , то существует также интеграл
, то существует также интеграл 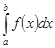 и для любых чисел
и для любых чисел 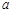 ,
, 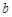 ,
, 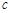
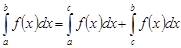 .
.
►Действительно, предел интегральной суммы не зависит от способа разбиения отрезка 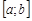 на частичные отрезки и от выбора
на частичные отрезки и от выбора 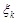 . Это позволяет при составлении интегральной суммы включить точку
. Это позволяет при составлении интегральной суммы включить точку 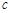 в число точек разбиения. Пусть
в число точек разбиения. Пусть 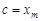 , т.е.
, т.е.
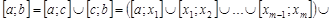
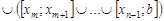 .
.
Тогда 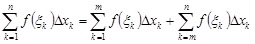 .
.
Переходя к пределу при 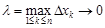 , получим
, получим
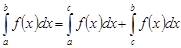 . ◄
. ◄
7 (интегрирование неравенств). Если 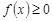
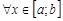 , то
, то 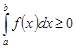 ,
, 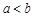 .
.
►Действительно, так как 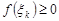 и
и 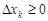 , то интегральная сумма
, то интегральная сумма 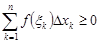 . Переходя к пределу в последнем равенстве, имеем
. Переходя к пределу в последнем равенстве, имеем
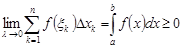 . ◄
. ◄
8 (монотонность). Если интегрируемые функции 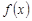 и
и 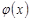 удовлетворяют неравенству
удовлетворяют неравенству 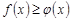
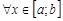 , то
, то
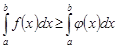 ,
, 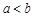 .
.
►Действительно, так как 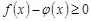
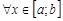 , то, согласно свойствам 5 и 7, имеем
, то, согласно свойствам 5 и 7, имеем
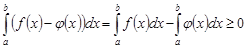 .
.
Следовательно 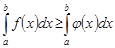 .◄
.◄
Замечание. Так как 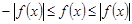
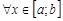 , то
, то
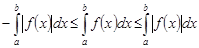 .
.
Отсюда 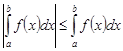 .
.
 2015-04-17
2015-04-17 13667
13667
