2015-04-17
763
Если функция 
непрерывна на отрезке 
и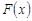 
– какая-нибудь первообразная на этом отрезке, то справедлива формула Ньютона-Лейбница
.
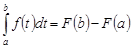►Пусть функция 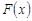является первообразной функции на отрезке . Если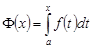 
другая первообразная функции на отрезке , то они отличаются на некоторую постоянную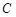 
и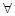 
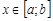имеет место равенство
.
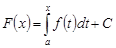Положим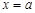 
и, учитывая, что 
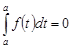, получим 
.
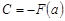Подставляя это значение вместо 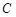, имеем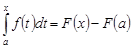 
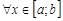. Тогда при 
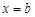получаем . ◄
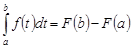Замечание. Формула Ньютона – Лейбница называется основной формулой интегрального исчисления. Иногда ее удобно записывать в виде:
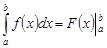
Вопрос4 Ряды действительных и комплексных чисел. Признаки сходимости действительных положительных и знакопеременных рядов. Степенные ряды и их область сходимости.
