2015-04-17
1481
Теорема 4Для того чтобы ряд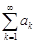 
с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм 
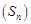этого ряда была ограничена.
Теорема 5 (интегральный признак Коши) Если неотрицательная интегрируемая функция 
на промежутке 
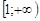монотонно убывает, и члены ряда 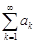имеют вид 
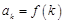, то ряд 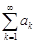и несобственный интеграл 
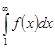сходятся или расходятся одновременно, причем в случае сходимости имеет место неравенство:
.
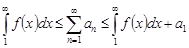Теорема 6 (признак сравнения) Пусть для членов рядов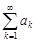 
и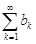 
справедливо неравенство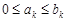 
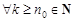. Тогда:
1) если ряд 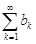сходится, то и ряд 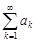сходится,
2) если ряд 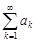расходится, то и ряд 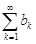расходится.
Следствие (предельный признак сравнения) Пусть для членов рядов (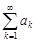
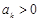) и (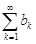
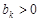) существует конечный предел:
, 
.
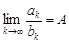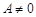Тогда ряды 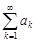и 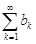сходятся и расходятся одновременно.
Для исследования на сходимость рядов с помощью признаков сравнения используются ряды:
– ряд из элементов геометрической прогрессии: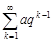 
, 
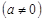, сходящийся при 
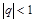и расходящийся при 
;
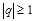– обобщенный гармонический ряд: 
, сходящийся при 
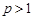и расходящийся при 
.
|
|
|
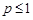Теорема 7 (признак Д’аламбера) Пусть для ряда (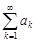
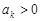) существует предел
.
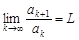Тогда при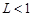 
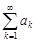ряд сходится, а при 
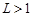ряд 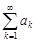расходится.
Вопрос о сходимости ряда остается открытым, если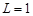 
.
Теорема 8 (признак Коши) Пусть для ряда 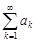(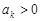) существует предел
.
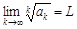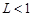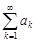Тогда при ряд сходится, а при 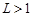ряд 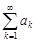расходится.
Вопрос о сходимости ряда остается открытым, если .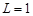
Из существования предела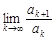 
следует, что существует и предел 
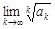. Обратное утверждение не всегда имеет место, т. е. признак Коши «сильнее» признака Д’аламбера
