Знакочередующиеся ряды, признак Лейбница

Знакочередующимся называется ряд, все члены которого поочередно меняют знак:

,

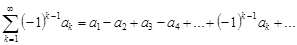где 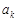, , 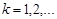– числа одного знака.

Теорема 1 (признак Лейбница) Пусть члены знакочередующегося ряда 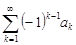удовлетворяют условиям:

1) ;

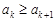
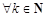2) .

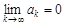Тогда ряд 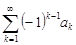сходится, а его сумма 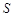не превосходит первого члена, т. е. .

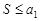Ряд, удовлетворяющий условиям теоремы 1 называется рядом Лейбница.

Остаток 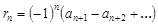ряда Лейбница удовлетворяет неравенству .

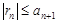Ряды, содержащие как положительные, так и отрицательные члены, называются знакопеременными.