2015-04-17
1479
Теорема 3. Если функция 
непрерывна во всех отрезка точках некоторого промежутка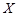 
, то на этом промежутке у нее существует первообразная. При этом для любой точки 
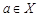функция 
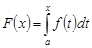является одной из первообразных функций на промежутке .
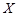► Если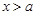 
, 
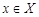, то равенство 
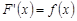следует из теоремы 2.
Если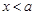 
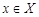, , то
. ◄
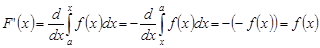Замечание. Совокупность всех первообразных непрерывной на некотором промежутке 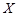функции представляет собой неопределенный интеграл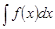 
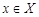, . Определенный интеграл 
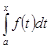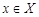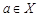, , , является одной из первообразных функции на .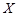
Поэтому
.
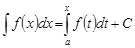Таким образом, установлена связь между неопределенным и определенным интегралами.
