Ряд
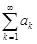 ,
, 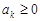
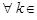
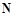
называется рядом с неотрицательными членами.
Для рядов с неотрицательными членами справедливы следующие свойства:
– перестановка, отбрасывание или добавление конечного числа членов ряда не влияет на его сходимость (расходимость);
– если ряды 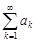 и
и 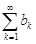 сходятся и их суммы равны
сходятся и их суммы равны 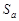 и
и 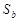 соответственно, то ряд
соответственно, то ряд 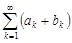 также сходится и
также сходится и
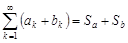 .
.
Ряд 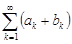 называется суммой рядов
называется суммой рядов 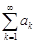 и
и 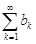 ;
;
– если ряд 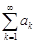 сходится и его сумма равна
сходится и его сумма равна 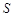 , то ряд
, то ряд 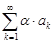 также сходится и
также сходится и
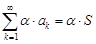 .
.
Ряд 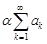 называется произведением ряда
называется произведением ряда 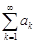 на число
на число 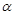 ;
;
– если ряд 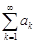 сходится, то и ряд, полученный группировкой его членов без изменения порядка их расположения, также сходится и имеет ту же сумму, что и исходный ряд.
сходится, то и ряд, полученный группировкой его членов без изменения порядка их расположения, также сходится и имеет ту же сумму, что и исходный ряд.
Теорема 3 (критерий Коши сходимости ряда) Для того чтобы ряд 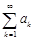 сходился, необходимо и достаточно, чтобы для любого
сходился, необходимо и достаточно, чтобы для любого 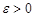 существовало такое число
существовало такое число 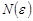 , что для всех
, что для всех 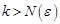 и всех
и всех 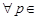
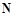 имело место неравенство:
имело место неравенство:
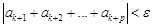 .
.
 2015-04-17
2015-04-17 650
650








