Ряд 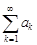 называется абсолютно сходящимся, если ряд с неотрицательными членами
называется абсолютно сходящимся, если ряд с неотрицательными членами 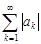 сходится.
сходится.
Теорема 2 Если ряд абсолютно сходится, то он сходится.
Обратное утверждение в общем случае не имеет места.
Абсолютно сходящиеся ряды обладают свойствами:
– если ряд 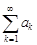 абсолютно сходится и
абсолютно сходится и 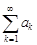 =
= 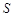 ,
, 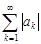 =
= 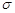 , то
, то 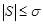 ;
;
– если ряды 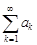 и
и 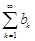 абсолютно сходятся, то при любых
абсолютно сходятся, то при любых 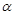 и
и 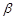 ряд
ряд 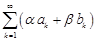 абсолютно сходится;
абсолютно сходится;
– если ряд 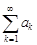 абсолютно сходится, то ряд, составленный из тех же членов, но взятых в другом порядке, также абсолютно сходится и его сумма равна сумме исходного ряда;
абсолютно сходится, то ряд, составленный из тех же членов, но взятых в другом порядке, также абсолютно сходится и его сумма равна сумме исходного ряда;
– если ряды 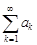 и
и 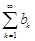 абсолютно сходятся, то ряд, составленный из всевозможных попарных произведений
абсолютно сходятся, то ряд, составленный из всевозможных попарных произведений 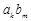 членов этих рядов, расположенных в любом порядке, также абсолютно сходится.
членов этих рядов, расположенных в любом порядке, также абсолютно сходится.
Если ряд 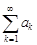 сходится, а ряд
сходится, а ряд 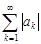 расходится, то ряд
расходится, то ряд 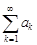 называется условно сходящимся.
называется условно сходящимся.
Для ряда 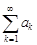 обозначим через
обозначим через 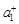 ,
, 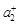 , …,
, …, 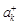 ,… и
,… и 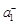 ,
, 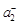 , …,
, …, 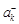 , … соответственно его неотрицательные и отрицательные члены, взятые в том же порядке, в котором они расположены в ряде
, … соответственно его неотрицательные и отрицательные члены, взятые в том же порядке, в котором они расположены в ряде 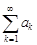 . Рассмотрим ряды
. Рассмотрим ряды 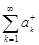 и
и 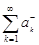 , члены которых неотрицательны.
, члены которых неотрицательны.
Теорема 3 Если ряд 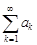 условно сходится, то оба ряда
условно сходится, то оба ряда 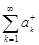 и
и 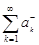 расходятся.
расходятся.
Теорема 4 (Римана) Если ряд 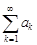 условно сходится, то, каково бы ни было действительное число
условно сходится, то, каково бы ни было действительное число 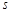 , можно так переставить его члены, что сумма получившегося ряда будет равна
, можно так переставить его члены, что сумма получившегося ряда будет равна 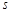
 2015-04-17
2015-04-17 1737
1737
