Степенные ряды. Ряд вида называется степенным рядом по степеням

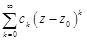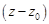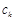
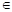
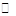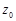
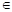
Ряд вида называется степенным рядом по степеням . Здесь – коэффициенты ряда, 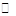– фиксированная точка.

Теорема 3 (Абеля) Если степенной ряд 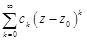сходится в точке 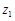, то он сходится во всех точках 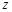, удовлетворяющих условию 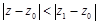, причем сходимость будет равномерной в любом круге 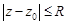, 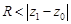. Если степенной ряд 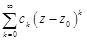расходится в точке 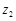, то он расходится во всех точках 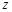, удовлетворяющих условию .

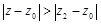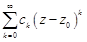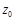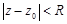Для степенного ряда , имеющего как точки сходимости (кроме , где ряд всегда сходится), так и точки расходимости, всегда существует такое действительное число , что внутри круга ряд сходится, а вне этого круга – расходится.

Область 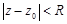называется кругом сходимости, а число 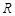– радиусом сходимости степенного ряда.

Радиус сходимости 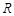вычисляется:

– по формуле Коши-Адамара ,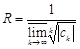

– по формуле 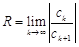, если этот предел существует.

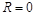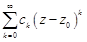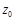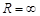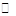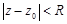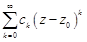Если , то ряд сходится лишь в точке ; если , то ряд сходится на всей комплексной плоскости .Внутри круга сходимости ряд сходится к аналитической функции. Степенной ряд внутри круга сходимости можно почленно интегрировать и почленно дифференцировать любое число раз. При этом радиус сходимости каждого вновь полученного ряда равен радиусу сходимости исходного ряда, а над суммой ряда выполняется то же действие, что и над самим рядом