Из школьного курса известно уравнение прямой линии с угловым коэффициентом:
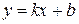 , (3.5)
, (3.5)
где число k, называемое угловым коэффициентом прямой, равно тангенсу угла наклона прямой к оси Ox, а число b равно величине отрезка, отсекаемого прямой на оси Oy.
Вертикальные прямые перпендикулярны оси Ox и, следовательно, не имеют углового коэффициента. Вертикальная прямая линия имеет уравнение вида 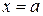 , где а – некоторая константа. Кстати, если положить в уравнении (3.5)
, где а – некоторая константа. Кстати, если положить в уравнении (3.5) 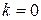 , то мы получим уравнение горизонтальной прямой линии:
, то мы получим уравнение горизонтальной прямой линии: 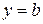 .
.
В любом случае уравнение прямой линии является уравнением первой степени. Общим уравнением прямой линии называется уравнение
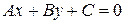 , (3.6)
, (3.6)
где А, В и С – постоянные числа, причем коэффициенты А и В не равны нулю одновременно: 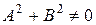 . Если в уравнении (3.6) коэффициент В отличен от нуля, то данное уравнение можно записать в виде
. Если в уравнении (3.6) коэффициент В отличен от нуля, то данное уравнение можно записать в виде 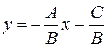 . Сравнивая полученное уравнение с (3.5), получим полезную формулу:
. Сравнивая полученное уравнение с (3.5), получим полезную формулу:
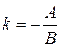 . (3.7)
. (3.7)
Если в уравнении (3.6) коэффициент В = 0, то данное уравнение задает вертикальную прямую: 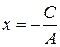 .
.
Предположим, что прямая линия проходит через заданную точку 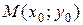 и имеет угловой коэффициент k. Подставим координаты точки М в уравнение (3.5):
и имеет угловой коэффициент k. Подставим координаты точки М в уравнение (3.5): 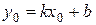 . Вычитая полученное равенство из равенства (3.5), мы получим уравнение прямой, проходящей через заданную точку, с заданным угловым коэффициентом:
. Вычитая полученное равенство из равенства (3.5), мы получим уравнение прямой, проходящей через заданную точку, с заданным угловым коэффициентом:
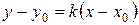 . (3.8)
. (3.8)
Предположим, что прямая линия проходит через две точки 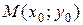 и
и 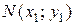 . Предположим сначала, что x 1 ¹ x 0, т. е. прямая MN не параллельна оси Oy. В уравнение (3.8) вместо текущих координат подставим координаты точки N:
. Предположим сначала, что x 1 ¹ x 0, т. е. прямая MN не параллельна оси Oy. В уравнение (3.8) вместо текущих координат подставим координаты точки N: 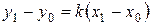 . Из полученного равенства найдем угловой коэффициент прямой, проходящей через две заданные точки:
. Из полученного равенства найдем угловой коэффициент прямой, проходящей через две заданные точки:
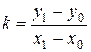 . (3.9)
. (3.9)
Подставляя найденный угловой коэффициент в уравнение (3.8) (в предположении, что y 1 ¹ y 0), мы получим уравнение прямой, проходящей через две заданные точки:
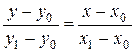 . (3.10)
. (3.10)
Если x 1 = x 0, то прямая MN параллельна оси Oy, и уравнение этой прямой, очевидно, будет x = x 0.
Если y 1 = y 0, то прямая MN параллельна оси Ox, и уравнение этой прямой будет y = y 0.
g Угол между двумя прямыми 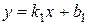 и
и 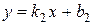 находится по формуле:
находится по формуле:
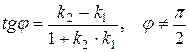 . (3.11)
. (3.11)
Точнее, по формуле (3.11) можно найти тот угол между прямыми, который получается при повороте прямой 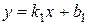 против часовой стрелки вокруг точки пересечения прямых, до совмещения с прямой
против часовой стрелки вокруг точки пересечения прямых, до совмещения с прямой 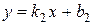 .
.
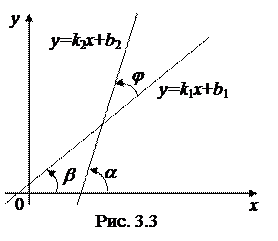 4Для доказательства формулы (3.11) достаточно заметить, что угол j является разностью углов a и b, которые образуют с осью Ox соответственно прямые
4Для доказательства формулы (3.11) достаточно заметить, что угол j является разностью углов a и b, которые образуют с осью Ox соответственно прямые 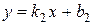 и
и 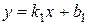 (рис. 3.3). Таким образом, подставляя
(рис. 3.3). Таким образом, подставляя 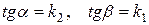 в формулу
в формулу 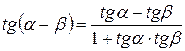 , получим:
, получим:
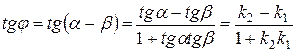 .3
.3
Замечание. Формула (3.11) имеет место только в том случае, когда обе прямые имеют угловые коэффициенты. Читателям мы предлагаем самостоятельно вывести формулу для нахождения угла между вертикальной прямой x = a и наклонной прямой y = kx + b.
Из формулы (3.11) вытекают два важных следствия:
1. Условие параллельности двух прямых.
g Две прямые, имеющие угловые коэффициенты k 1 и k 2 параллельны, тогда и только тогда, когда k 1 = k 2. 4Действительно, для параллельных прямых 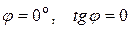 и, следовательно, k 1 = k 2. Обратное утверждение очевидно.3
и, следовательно, k 1 = k 2. Обратное утверждение очевидно.3
2. Условие перпендикулярности двух прямых.
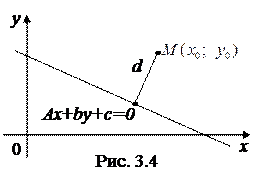 g Две прямые, имеющие угловые коэффициенты k 1 и k 2 перпендикулярны, тогда и только тогда, когда
g Две прямые, имеющие угловые коэффициенты k 1 и k 2 перпендикулярны, тогда и только тогда, когда 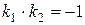 . 4Действительно, для перпендикулярных прямых
. 4Действительно, для перпендикулярных прямых 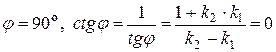 . Таким образом,
. Таким образом, 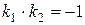 .3
.3
1 Расстояние от точки 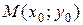 до прямой линии
до прямой линии 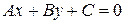 (рис. 3.4) можно найти по формуле:
(рис. 3.4) можно найти по формуле:
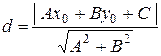 . (3.12)
. (3.12)
Задача 3.2. Дан треугольник A (2; 7), B (-5; 7), C (5; 3). Найти:
1) уравнения сторон; 2) уравнение и длину медианы AM; 3) уравнение и длину высоты BD; 4) уравнение биссектрисы AK; 5) точку пересечения медианы AM с высотой BD и угол между ними.
Решение. 1) Уравнения сторон AC и BC найдем, используя уравнение прямой, проходящей через две точки (3.10):
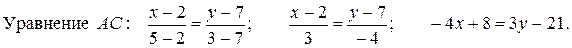
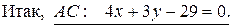
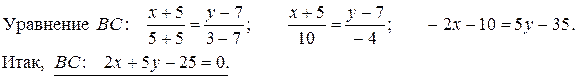
Уравнение AB находится еще проще. Нужно только заметить, что вторая координата точек A и B одинакова и равна 7.
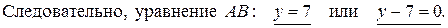
2) Найдем точку M – середину стороны BC:
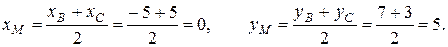
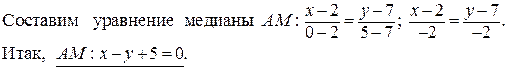
Длину медианы найдем как расстояние между двумя точками:
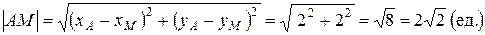 .
.
3) Определим угловой коэффициент стороны AC. Для того уравнение
AC запишем в виде 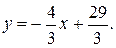 Следовательно,
Следовательно, 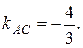
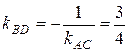 (условие перпендикулярности прямых BD и AC).
(условие перпендикулярности прямых BD и AC).
Составим уравнение высоты BD, используя уравнение (3.8) прямой, проходящей через заданную точку B и с угловым коэффициентом k.
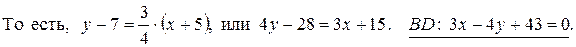
Длину высоты BD найдем как расстояние точки B до прямой AC по формуле (3.12):
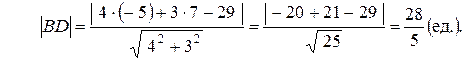
4) Найдем основание биссектрисы (точку K), используя то, что точка K делит отрезок BC на части, пропорциональные прилежащим сторонам треугольника: 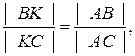
где 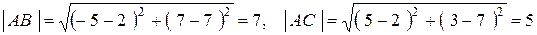 .
.
Следовательно, 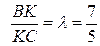 .
.
Для нахождения координат точки K используем формулы (3.2) деления отрезка в данном отношении:
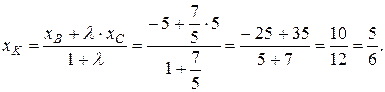
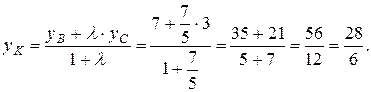
Составим уравнение AK, используя координаты точек A и K:
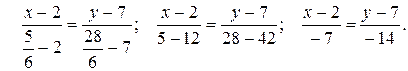
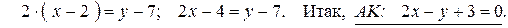
5) Найдем точку пересечения медианы AM с высотой BD, решив систему:
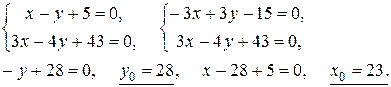 .
.
Итак, точка O пересечения медианы с высотой имеет координаты:
O (23; 28). Для нахождения угла между прямыми линиями BD и AM воспользуемся формулой (3.11), взяв в качестве углового коэффициента
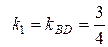 и
и 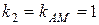 .
.
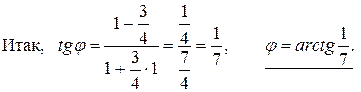
 2015-04-01
2015-04-01 1950
1950
