Операции над векторами и их свойства

1. Умножение вектора на число. 2 Для того чтобы умножить вектор на число l необходимо:

1) Длину вектора «увеличить» в | l | раз (уменьшить, если | l | < 1).

2) Направление вектора оставить прежним (таким же, как у вектора ), если l > 0, или изменить на противоположное, если l < 0. Данное определение распространяется как на вектора, расположенные на плоскости, так и в пространстве.

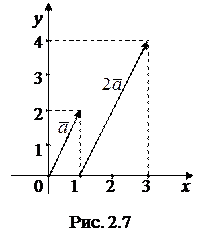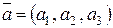Из рисунка 2.7 видно, что при умножении вектора на число, его координаты умножаются на это число. Действительно, величины проекций вектора 2 на оси координат в два раза больше величин проекций вектора . В общем случае, если вектор имеет координаты , то вектор .

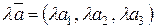2. Сложение векторов. 2 Суммой двух векторов и называют такой третий вектор 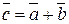, выходящий из их общего начала, и служащий диагональю параллелограмма, сторонами которого являются векторы и (правило параллелограмма) (рис. 2.8).

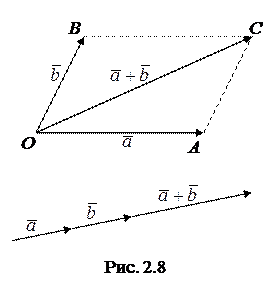Если же два вектора и после приведения их к общему началу лежат на одной прямой, то их сумма 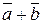по определению называется вектор 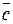, длина которого равна сумме длин слагаемых векторов и направление совпадает с направлением этих векторов, если последние одинаково направлены; если же слагаемые векторы направлены в разные стороны, то их сумма есть вектор 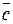, длина которого равна разности длин слагаемых векторов и направление совпадает с направлением вектора, имеющего большую длину. В случае равенства длин двух противоположно направленных векторов их сумма равна вектору, длина которого равна нулю. Такой вектор называют нулевым вектором и обозначают .

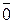1 Если векторы 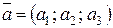и 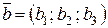заданы своими координатами, то координаты их суммы равны сумме соответствующих координат слагаемых векторов: .

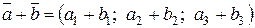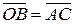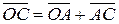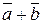Из рис. 2.8 видно, что и, следовательно, . Отсюда вытекает еще одно правило сложения векторов (правило треугольника): если начало вектора совместить с концом вектора , то суммой векторов будет вектор, начало которого совпадает с началом вектора , а конец,– с концом вектора .

g Операция сложения обладает следующими свойствами:

1. .

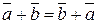2. .

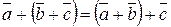Первое свойство очевидно. Второе свойство докажем используя правило треугольника сложения векторов (рис. 2.9).

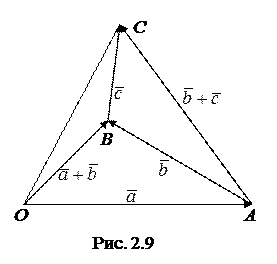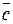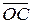4 Совместим начало вектора с концом вектора , а начало вектора с концом вектора . Тогда вектор , начало которого совпадает с началом вектора , а конец,– с концом вектора 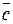можно найти двумя способами. С одной стороны 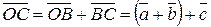, а с другой стороны 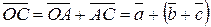. 3

3. Вычитание векторов. Данная операция в специальном определении не нуждается, так как разность 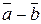можно рассматривать как последовательное выполнение двух уже известных операций: умножение вектора на –1 и сложение векторов. То есть .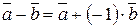

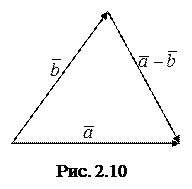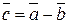g Если совместить начала векторов и , то вектор будет иметь начало в конце вектора-вычитаемого (), а конец,– в конце вектора-уменьшаемого ().

4 Для доказательства достаточно воспользоваться тем, что вектор 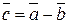, будучи сложенным с вектором , дает вектор (рис. 2.10). 3

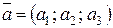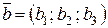Если векторы и имеют координаты , , то координаты их разности равны разности соответствующих координат вычитаемых векторов: .

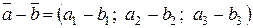4. 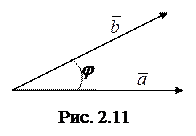Скалярное произведение векторов.

2 Скалярным произведением вектора на вектор (обозначается 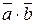) (рис. 2.11) называется число равное произведению длин векторов 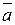и на косинус угла между ними:

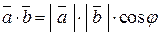. (2.3)
Из школьного курса известно, что скалярное произведение можно вычислить, зная координаты векторов 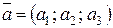и 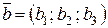. А именно:

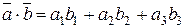. (2.4)
Из формул (2.1) – (2.4) вытекает одна очень полезная формула, позволяющая находить углы между векторами, заданными своими координатами:

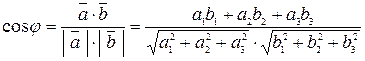(2.5)

1 Скалярное произведение обладает следующими свойствами:

1. 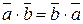(скалярное произведение коммутативно).

2. 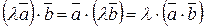(постоянный множитель можно выносить за знак скалярного произведения).

3. .

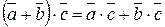4. 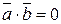тогда и только тогда, когда векторы 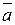и взаимно перпендикулярны (нулевой вектор считается перпендикулярным любому вектору).

Все перечисленные выше свойства вытекают из определения скалярного произведения и проверяются непосредственно.

5. Проекция вектора на ось. 2 Пусть задан вектор 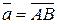и пусть P и Q являются проекциями точек А и В, соответственно, на заданную числовую ось (с). Проекцией вектора 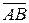на ось (с) называется величина направленного отрезка .

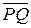Из определения следует, что Пр_(с) 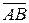= вел. 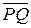= | |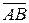×cos j = | |×cos j,
где j – угол, который образует вектор 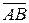с осью (с).

Если на оси (с) взять произвольный вектор , направленный в ту же сторону, что и ось (с), то угол j можно найти как угол между векторами и по формуле (2.5). Тогда

Пр_(с) 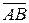= 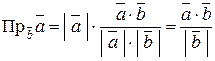. (2.6)
Формула (2.6) позволяет найти проекцию вектора на направление вектора .

6. 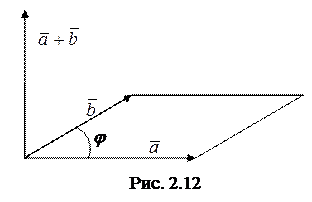Векторное произведение векторов.

2 Векторным произведением вектора на вектор (обозначается 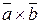) называется вектор 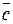, длина которого численно равна площади параллелограмма, построенного на векторах и , перпендикулярного обоим векторам и , и направленного так, что из его конца кратчайший поворот от вектора к вектору виден против часовой стрелки (векторы , и 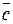образуют правую тройку) (рис 2.12).

1 Отметим ряд свойств непосредственно вытекающих из определения векторного произведения:

1. .

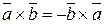2. .

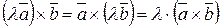3. .

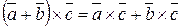4. 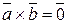тогда и только тогда, когда векторы 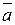и коллинеарны (лежат на параллельных прямых). Нулевой вектор считается коллинеарным любому вектору. Координаты коллинеарных векторов пропорциональны.

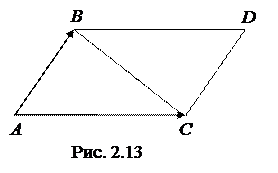Векторное произведение чаще всего используют при нахождении площади параллелограмма и треугольника (рис 2.13). Непосредственно из определения следуют две формулы:

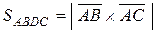, (2.7)
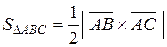. (2.8)
В качестве наиболее простого примера рассмотрим всевозможные векторные произведения единичных векторов 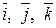, расположенных на осях координат Ox, Oy и Oz, соответственно:

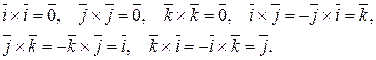(2.9)
Выведем формулу для нахождения векторного произведения двух произвольных векторов, заданных своими координатами. Пусть даны два вектора 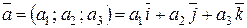и 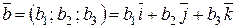. Пользуясь свойствами векторного произведения, найдем .

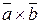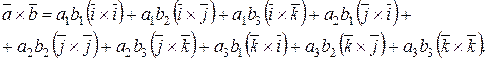(2.10)
Подставляя в (2.10) равенства (2.9) и приводя подобные члены, получим:

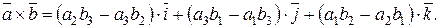(2.11)
Или в более компактной форме

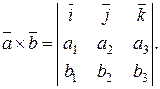(2.12)

7. Смешанное произведение векторов.

Смешанным произведением трех векторов 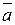, и 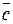называется векторно-скалярное произведение 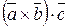. Смешанное произведение является числом. Вычислим это число, зная координаты векторов 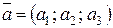, 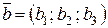и 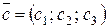. Из формулы (2.11) следует, что 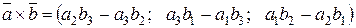. Далее по формуле (2.4) получим:

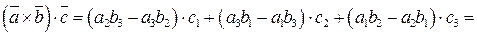
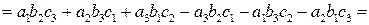
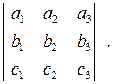
Аналогичный результат получится, если вычислить 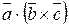(проверьте самостоятельно). Таким образом, мы приходим к выводу, что
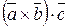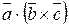= . Благодаря этому свойству смешанное произведение принято обозначать символом 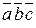. Мы доказали, что

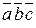
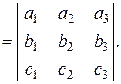(2.13)
Так как при перестановке двух строк определитель меняет знак, то

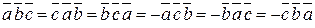. (2.14)

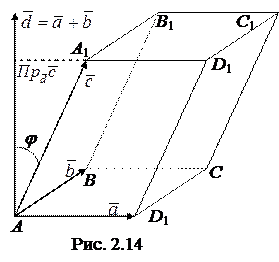Таким образом, при перестановке вектора из конца смешанного произведения в начало, векторное произведение не меняет своего знака. А при перестановке двух соседних сомножителей, смешанное произведение меняет знак на противоположный.

g Модуль смешанного произведения 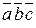численно равен объему параллелепипеда, построенного на векторах 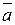, и .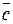

4По определению скалярного произведения:

= ,

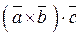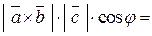
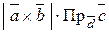где 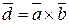, а j – угол между векторам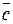и и 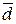. Следовательно,

,

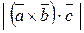
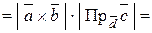
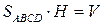где через H обозначена высота параллелепипеда, равная модулю проекции вектора 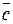на направление вектора 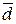, перпендикулярного плоскости основания параллелепипеда ABCD, V – объем параллелепипеда (рис. 2.14).3

Поскольку объем треугольной пирамиды, построенного на векторах 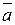, и 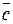, в шесть раз меньше объема соответствующего параллелепипеда, то

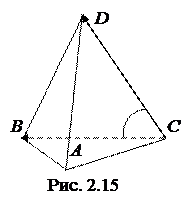
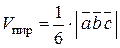(2.15)
Задача 2.2. Дана пирамида ABCD (рис. 2.15): A (2; 4; – 1), B (3; 2; 0), C (1; – 3; 2), D (5;-1; 3). Найти: 1) угол BCD; 2) площадь грани ABC; 3) объем пирамиды.