Общая теория кривых второго порядка

В общем случае уравнение кривой второго порядка выглядит следующим образом:

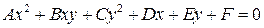. (3.32)
В уравнении (3.32) хотя бы один из коэффициентов A, B, C должен быть отличен от нуля, т.е. .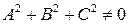

При различных сочетаниях коэффициетов, уравнение (3.32) может являться уравнением окружности, эллипса, гиперболы или параболы. Возможны так же вырожденные случаи:

1) Пара пересекающихся прямых (при этом уравнение (3.32) можно представить в ви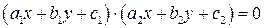де , где ).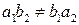

2) Пара параллельных прямых (при этом уравнение (3.32) можно представить в ви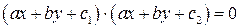де , где ).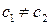

3) Пара совпадающих прямых (при этом уравнение (3.32) можно представить в виде ).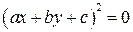

4) Точка (например, когда уравнение (3.32) можно представить в ви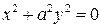де , где ).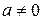

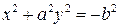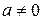5) Пустое множество (например, когда уравнение (3.32) можно представить в виде , где и ).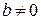

Уравнение (3.32) всегда можно привести к простешему (каноническому) виду, используя формулы параллельного переноса и поворота осей координат.

1. Формулы параллельного переноса координат.

Предположим, что на плоскости заданы две декартовы системы координат старая xOy и новая x'O'y'. Причем оси новой системы паралльны соответствыющим осям старой системы координат. Обозначим через 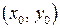старые координаты (относительно системы xOy) нового начала O'.

Возьмем на плоскости произвольную точку M и обозначим ее координаты относительно старой системы координат 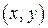, а относительно новой :

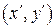Из рис. 3.11 видно, что старые координаты точки M 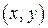связаны с новыми координатами 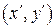формулами:

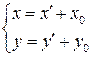, (3.33)
или, что тоже самое

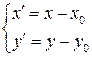. (3.34)
Формулы (3.33) позволяют найти старые координаты точки М через новые, а формулы (3.34) новые координаты через старые.

Если координаты центра эллипса или гиперболы и вершины параболы смещены в точку (x ₀; y ₀), то уравнения соответствующих кривых будут выглядеть следующим образом:

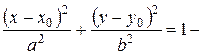уравнение эллипса, (3.35)

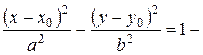уравнение гиперболы, (3.36)

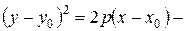уравнение параболы. (3.37)

Задача 3.5. Найти координаты фокусов и уравнение директрисы параболы, заданной уравнением: y = 4 x ² + 12 x – 5.

Решение. Выделим полный квадрат по переменной x в уравнении параболы:

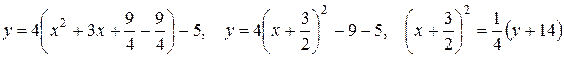Мы получили уравнение параболы, вершина которой смещена в точку 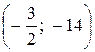, а параметр находится из равенства 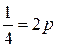. Откуда .

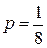Так как ветви параболы направлены вверх, то фокус параболы находится выше ее вершины на величину 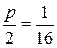. Таким образом, координаты фокуса параболы равны: 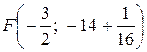или .

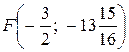Уравнение директрисы будет 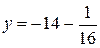или .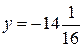

2. Формулы поворота системы координат.

Предположим, что на плоскости заданы две декартовы системы координат старая xOy и новая x'Oy'. Причем оси новой системы повернуты относительно осей старой системы координат против часовой стрели на угол a. Начала старой и новой систем координат совпадают.

Возьмем на плоскости произвольную точку M и обозначим ее координаты относительно старой системы координат 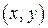, а относительно новой 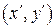(рис. 3.12).

Напишем без вывода формулы поворота координатных осей, позволяющие находить старые координаты точки М 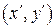через новые координаты 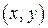(формулы (3.38)), и наоборот старые координаты через новые (формулы (3.39)):

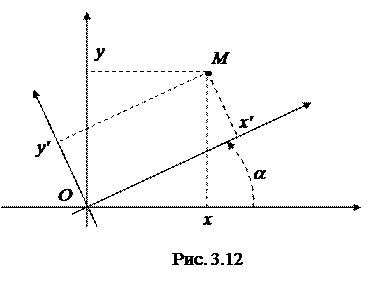
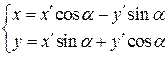, (3.38)

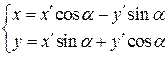. (3.39)

Если в уравнение кривой второго порядка (3.32) вместо старых текущих координат 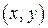подставить их выражения через новые координаты (формулы (3.33) или (3.38)), то мы получим уравнение той же кривой относительно новой системы координат (смещенной или повернутой, соответсвенно):

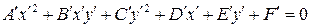. (3.40)

Обычно преобразование системы координат производят в два этапа:

1) Сначала производят поворот системы координат, используя формулы (3.38). При этом добиваются того, чтобы новый коэффициент 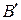при произведении 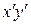стал равен нулю. Это всегда можно сделать, взяв в качестве угла a любое решение уравнения

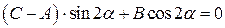(3.41)
2) Затем совершают параллельный перенос системы координат :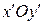

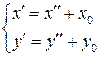, (3.42)

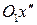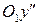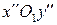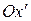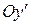где оси и системы координат параллельны осям и (соответственно), а 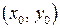– координаты нового начала координат О ₁ относительно системы .

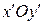Задача 3.6. Определить тип кривой второго порядка и изобразить ее в декартовой системе координат:

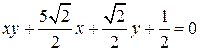. (3.43)

Решение. В данном общем уравнении кривой второго порядка коэффициентами являются 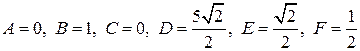. Следовательно, уравнение (3.41) примет вид: 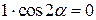. Одним из решений данного уравнения является a = 45°. При этом формулы поворота системы координат (3.38) будут выглядеть следующим образом:

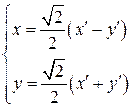. (3.44)

Подставив x и y из формул (3.44) в уравнение (3.43) получим:

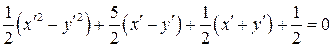. Умножим обе части полученного уравнения на 2 и раскроем скобки. Получим уравнение, в котором отсутствует произведение x ' y ':

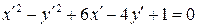Для дальнейшего упрощения уравнения используем формулы параллельного переноса координат (3.42). После чего уравнение примет вид:

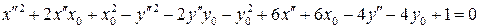или

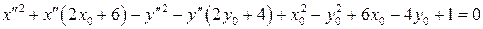. (3.45)

Уравнение (3.45) максимально упростится, если точку 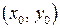выбрать так, чтобы выполнялась система: 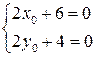. Решением данной системы является 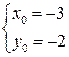. Подставляя найденные координаты нового начала координат О ₁ в уравнение (3.45), получим:

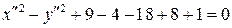или

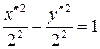Полученное уравнение является уравнением гиперболы, оси которой расположены на осях координат 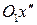и 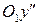. Асимптоты гиперболы параллельны старым осям координат 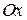и .