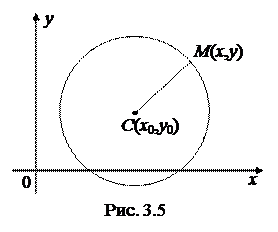 1. Окружность. 2 Окружностью называется геометрическое место точек, равноудаленных от одной фиксированной точки, называемой центром окружности. Расстояние от произвольной точки окружности до его центра называется радиусом окружности.
1. Окружность. 2 Окружностью называется геометрическое место точек, равноудаленных от одной фиксированной точки, называемой центром окружности. Расстояние от произвольной точки окружности до его центра называется радиусом окружности.
g Если центр окружности находится в точке 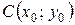 , а радиус равен R, то уравнение окружности имеет вид:
, а радиус равен R, то уравнение окружности имеет вид:
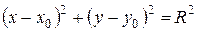 . (3.13)
. (3.13)
4Обозначим через 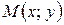 (рис. 3.5) произвольную точку окружности. Используя формулу расстояния между двумя токами (3.1) и определение окружности, получим:
(рис. 3.5) произвольную точку окружности. Используя формулу расстояния между двумя токами (3.1) и определение окружности, получим: 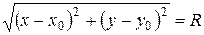 . Возводя полученное равенство в квадрат, мы получим формулу (3.13).3
. Возводя полученное равенство в квадрат, мы получим формулу (3.13).3
2. Эллипс. 2 Эллипсом называется геометрическое место точек, сумма расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
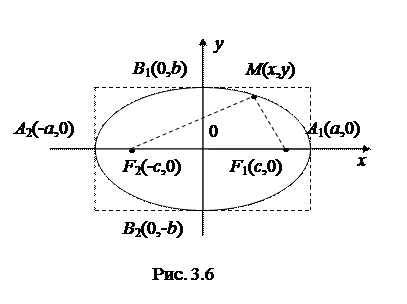 Для того, чтобы вывести каноническое (простейшее) уравнение эллипса, примем за ось Ox прямую, соединяющую фокусы F 1 и F 2. Пусть при этом фокусы будут симметричны относительно начала координат, т.е. будут иметь координаты:
Для того, чтобы вывести каноническое (простейшее) уравнение эллипса, примем за ось Ox прямую, соединяющую фокусы F 1 и F 2. Пусть при этом фокусы будут симметричны относительно начала координат, т.е. будут иметь координаты: 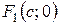 и
и 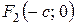 . Здесь через 2 с обозначено расстояние между фокусами. Обозначим через x и y координаты произвольной точки М эллипса (рис 3.6). Тогда по определению эллипса, сумма расстояний от точки М до точек F 1 и F 2 равно константе (обозначим эту константу через 2 а).
. Здесь через 2 с обозначено расстояние между фокусами. Обозначим через x и y координаты произвольной точки М эллипса (рис 3.6). Тогда по определению эллипса, сумма расстояний от точки М до точек F 1 и F 2 равно константе (обозначим эту константу через 2 а).
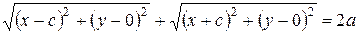 . (3.14)
. (3.14)
Уравнение (3.14) является уравнением эллипса. Упростим данное уравнение, избавившись от квадратных корней. Для этого перенесем один из радикалов в правую часть равенства (3.14) и возведем обе части полученного равенства в квадрат:
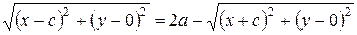 ,
,
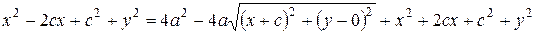 ,
,
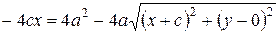 ,
,
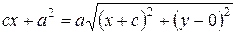 .
.
Возводя последнее равенство в квадрат, получим
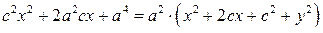 , или
, или
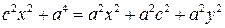 ,
,
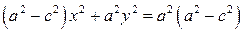 .
.
Разделим обе части на 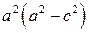 :
:
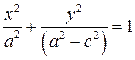 .
.
Так как сумма расстояний от произвольной точки эллипса до его фокусов больше расстояния между фокусами, т.е. 2 а > 2 c, то 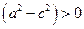 .
.
Обозначим 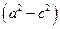 через b 2. Тогда простейшее (каноническое) уравнение эллипса будет иметь вид:
через b 2. Тогда простейшее (каноническое) уравнение эллипса будет иметь вид:
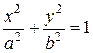 , (3.15)
, (3.15)
где положено
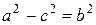 . (3.16)
. (3.16)
Оси координат являются осями симметрии эллипса, заданного уравнением (3.15). Действительно, если точка с текущими координатами (x; y) принадлежит эллипсу, то и точки 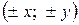 при любом сочетании знаков принадлежат эллипсу.
при любом сочетании знаков принадлежат эллипсу.
2Ось симметрии эллипса, на которой расположены фокусы, называется фокальной осью. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса. Подставляя x = 0 или y = 0 в уравнение эллипса найдем координаты вершин:
А 1(a; 0), А 2(– a; 0), B 1(0; b), B 2(0; – b).
2Отрезки А 1 А 2 и B 1 B 2, соединяющие противоположные вершины эллипса, а также их длины 2 a и 2 b, называют соответственно большой и малой осями эллипса. Числа a и b, называют соответственно большой и малой полуосями эллипса.
2Эксцентриситетом эллипса называется отношение расстояния между фокусами (2 с) к большой оси (2 a), т.е.
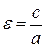 . (3.17)
. (3.17)
Так как а и с положительны, причем c < a, то эксцентриситет эллипса больше нуля, но меньше единицы (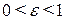 ).
).
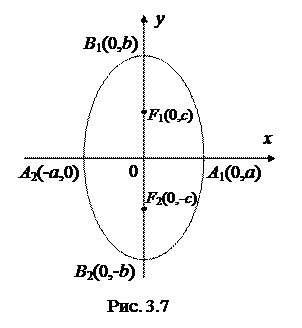 Если фокусы эллипса расположены на оси Oy (рис.3.7), то уравнение эллипса останется таким же, как и в предыдущем случае:
Если фокусы эллипса расположены на оси Oy (рис.3.7), то уравнение эллипса останется таким же, как и в предыдущем случае:
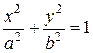 .
.
Однако в этом случае полуось b будет больше, чем a (эллипс вытянут вдоль оси Oy). Формулы (3.16) и (3.17) претерпят следующие изменения соответственно:
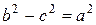 . (3.18)
. (3.18)
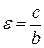 . (3.19)
. (3.19)
3. Гипербола. 2 Гиперболой называется геометрическое место точек, модуль разности расстояний которых до двух фиксированных точек, называемых фокусами, есть величина постоянная.
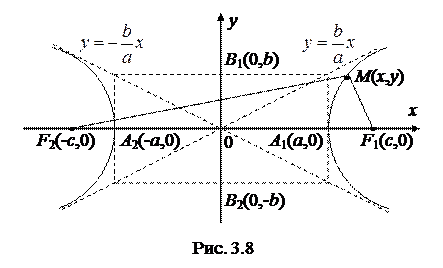 Выводится каноническое уравнение гиперболы аналогично тому как это делалось в случае эллипса. За ось Ox принимаем прямую, соединяющую фокусы F 1 и F 2 (рис.3.8). Пусть при этом фокусы будут симметричны относительно начала координат, т.е. будут иметь координаты:
Выводится каноническое уравнение гиперболы аналогично тому как это делалось в случае эллипса. За ось Ox принимаем прямую, соединяющую фокусы F 1 и F 2 (рис.3.8). Пусть при этом фокусы будут симметричны относительно начала координат, т.е. будут иметь координаты: 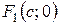 и
и 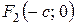 . Через 2 с, как и прежде, обозначено расстояние между фокусами.
. Через 2 с, как и прежде, обозначено расстояние между фокусами.
Обозначим через (x; y) координаты произвольной точки М гиперболы. Тогда по определению гиперболы, разность расстояний от точки М до точек F 1 и F 2 равно константе (обозначим эту константу через 2 а).
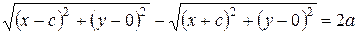 . (3.20)
. (3.20)
Производя преобразования аналогичные тем, которые применялись при упрощении уравнения эллипса, мы придем к каноническому уравнению гиперболы:
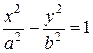 , (3.21)
, (3.21)
где положено
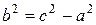 . (3.22)
. (3.22)
Оси координат являются осями симметрии гиперболы.
2Ось симметрии гиперболы, на которой расположены фокусы, называется фокальной осью. Точки пересечения гиперболы с ее осями симметрии называются вершинами гиперболы. С осью Oy гипербола не пересекается, т.к. уравнение 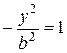 не имеет решения. Подставляя y = 0 в уравнение (3.21) найдем координаты вершин гиперболы: А 1(a; 0), А 2(– a; 0).
не имеет решения. Подставляя y = 0 в уравнение (3.21) найдем координаты вершин гиперболы: А 1(a; 0), А 2(– a; 0).
2Отрезок 2 a, длина которого равна расстоянию между вершинами гиперболы, называют действительной осью гиперболы. Отрезок 2 b называют мнимой осью гиперболы. Числа a и b, называют соответственно действительной и мнимой полуосями гиперболы.
Можно доказать, что прямые линии
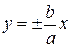 (3.23)
(3.23)
являются асимптотами гиперболы, т.е. такими прямыми, к которым неограниченно приближаются точки гиперболы при их неограниченном удалении от начала координат (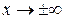 ).
).
2Эксцентриситетом гиперболы называется отношение расстояния между фокусами (2 с) к действительной оси (2 a), т.е., как и в случае эллипса
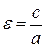 . (3.24)
. (3.24)
Однако в отличии от эллипса эксцентриситет гиперболы больше единицы.
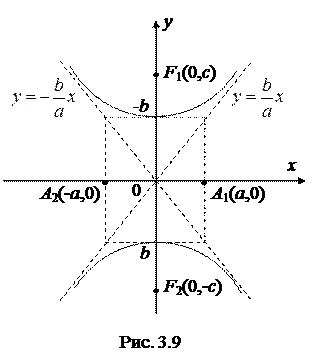 Если фокусы гиперболы расположены на оси Oy, то в левой части уравнения гиперболы изменятся знаки на противоположные:
Если фокусы гиперболы расположены на оси Oy, то в левой части уравнения гиперболы изменятся знаки на противоположные:
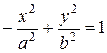 . (3.25)
. (3.25)
В этом случае полуось b будет действительной, а полуось a – мнимой. Ветви гиперболы будут симметричны относительно оси Oy (рис 3.9). Формулы (3.22) и (3.23) не изменятся, формула (3.24) будет выглядеть следующим образом:
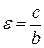 . (3.26)
. (3.26)
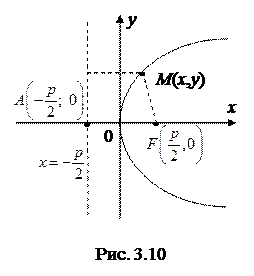 4. Парабола. Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом и от данной прямой, называемой директрисой (предполагается, что фокус не лежит на директрисе).
4. Парабола. Параболой называется геометрическое место точек, равноудаленных от данной точки, называемой фокусом и от данной прямой, называемой директрисой (предполагается, что фокус не лежит на директрисе).
Для того, чтобы составить простейшее уравнение параболы примем за ось Ox прямую, проходящую через ее фокус перпендикулярно директрисе, и направленную от директрисы к фокусу. За начало координат примем середину отрезка O от фокуса F до точки А пересечения оси Ox с директрисой. Длина отрезка AF обозначается через p и называется параметром параболы.
В данной системе координат координаты точек А и F будут, соответственно, 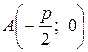 ,
, 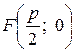 . Уравнение директрисы параболы будет
. Уравнение директрисы параболы будет 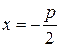 . Обозначим через (x; y) координаты произвольной точки М параболы (рис. 3.10). Тогда по определению параболы:
. Обозначим через (x; y) координаты произвольной точки М параболы (рис. 3.10). Тогда по определению параболы:
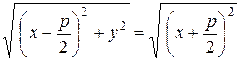 . (3.27)
. (3.27)
Возведем обе части равенства (3.27) в квадрат:
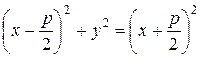 , или
, или
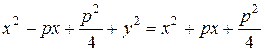 , откуда
, откуда
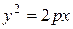 . (3.28)
. (3.28)
Уравнение (3.28) называется каноническим уравнением параболы.
Каноническими являются так же следующие уравнения параболы.
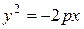 . (3.29)
. (3.29)
Ветви параболы, заданной уравнением (3.29), направлены влево, фокус имеет координаты 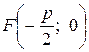 , уравнение директрисы
, уравнение директрисы 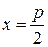 .
.
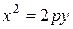 . (3.30)
. (3.30)
Ветви параболы, заданной уравнением (3.30), направлены вверх, фокус имеет координаты 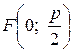 , уравнение директрисы
, уравнение директрисы 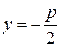 .
.
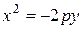 . (3.31)
. (3.31)
Ветви параболы, заданной уравнением (3.31), направлены вниз, фокус имеет координаты 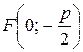 , уравнение директрисы
, уравнение директрисы 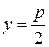 .
.
Задача 3.3. Найти координаты фокусов и эксцентриситет эллипса:
4 x 2+9 y 2 = 1.
Решение. В каноническом виде уравнение эллипса выглядит следующим образом: 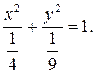 Из этого уравнения видно, что большая полуось эллипса равна
Из этого уравнения видно, что большая полуось эллипса равна 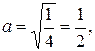 а малая полуось равна
а малая полуось равна 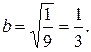 Расстояние от центра эллипса до его фокусов, находим из формулы (3.16):
Расстояние от центра эллипса до его фокусов, находим из формулы (3.16): 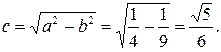 Таким образом, фокусы эллипса имеют координаты:
Таким образом, фокусы эллипса имеют координаты: 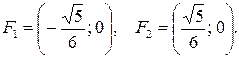
Эксцентриситет эллипса найдем по формуле (3.17):
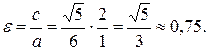
Задача 3.4. Асимптоты гиперболы имеют уравнения 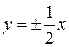 и расстояние между фокусами равно 10. Составить каноническое уравнение гиперболы.
и расстояние между фокусами равно 10. Составить каноническое уравнение гиперболы.
Решение. Из условия задачи следует, что
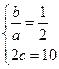 .
.
Подставляя в равенство (3.22) с = 5 и a = 2 b, мы получим уравнение, из которого найдем b:
b 2 = 25 – 4 b 2, 5 b 2 = 25, b 2 = 5, 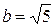 . Следовательно, a = 2 b =
. Следовательно, a = 2 b = 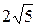 .
.
Подставляя a 2 = 20 и b 2 = 5 в уравнение (3.21), получим искомое уравнение гиперболы:
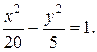
 2015-04-01
2015-04-01 3750
3750








