1. Область определения 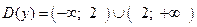 .
.
2. Пусть x = 0, тогда y = 1,5. Пусть y = 0, тогда x = 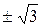 . То есть точки (0; 3/2) и (
. То есть точки (0; 3/2) и (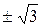 ; 0) – являются точками пересечения графика функции с осями координат. Если
; 0) – являются точками пересечения графика функции с осями координат. Если 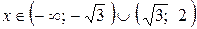 , то y (x) < 0. Если
, то y (x) < 0. Если 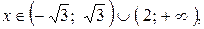 то y (x) > 0.
то y (x) > 0.
3. Функция общего вида, т. е. не является ни четной, ни нечетной. Действительно, 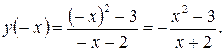 То есть y (- x) ¹ y (x) и y (- x)¹ - y (x).
То есть y (- x) ¹ y (x) и y (- x)¹ - y (x).
4. Функция не является периодической, так как она имеет только одну точку разрыва.
5. Функция непрерывна в области определения, так как является дробно-рациональной. Для исследования типа разрыва в точке x = 2 найдем односторонние пределы
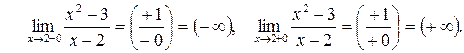
Следовательно, точка x = 2 является точкой разрыва второго рода, и прямая линия x = 2 является вертикальной асимптотой графика функции.
Уравнения наклонных (горизонтальных) асимптот графика функции будем искать в виде: y=kx+b, где k и b определяются по формулам (6.5) – (6.6):
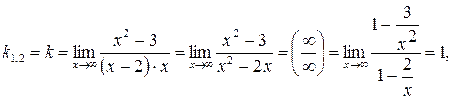
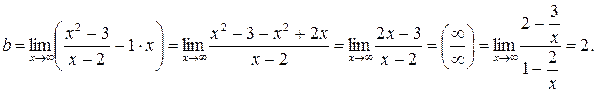
Таким образом, прямая y = x + 2 является наклонной асимптотой.
6. Найдем первую производную функции:
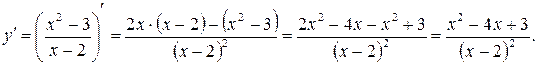
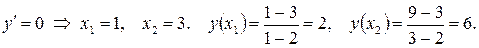
Итак, критическими точками 1-го рода являются точки x = 1 и x = 3. Точка x= 2 критической не является, т. к. она не принадлежит области определения функции.
7. Найдем вторую производную функции:
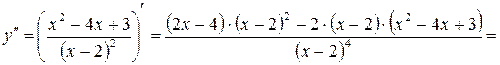
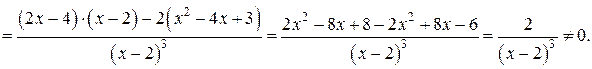
Критических точек второго рода функция не имеет.
8. Составим таблицу исследования функции:
| x | (–¥; 1) | (1; 2) | (2; 3) | (3; ¥) | |||
| y¢ (x) | + | – | Не сущ. | – | + | ||
| y² (x) | – | – | – | Не сущ. | + | + | + |
| y (x) | 
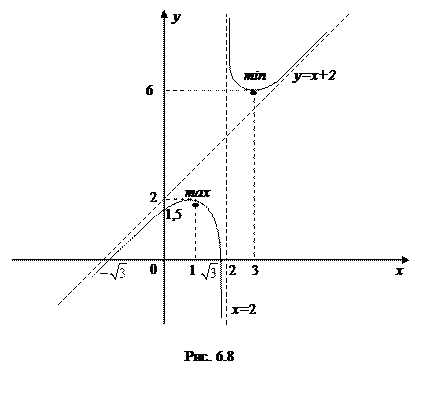
| max y = 2. | 
| Не сущ. | 
| min y = 6. | 
|
9. Построим график функции (рис.6.8):
 2015-04-01
2015-04-01 528
528








