Приведем без доказательства некоторые основные теоремы, справедливые для функций, непрерывных на отрезке.
1 Первая теорема Больцано-Коши. Пусть функция 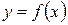 определена и непрерывна в замкнутом промежутке
определена и непрерывна в замкнутом промежутке 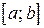 и на концах этого промежутка принимает значения разных знаков. Тогда между а и b найдется точка с, в которой функция обращается в нуль:
и на концах этого промежутка принимает значения разных знаков. Тогда между а и b найдется точка с, в которой функция обращается в нуль: 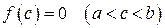 .
.
1 Вторая теорема Больцано-Коши. Пусть функция 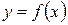 определена и непрерывна в некотором промежутке
определена и непрерывна в некотором промежутке 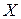 (замкнутом или нет, конечном или же бесконечном). Если в двух точках x = a и x = b (
(замкнутом или нет, конечном или же бесконечном). Если в двух точках x = a и x = b (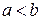 ) функция принимает неравные значения
) функция принимает неравные значения 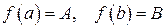 , то каково бы ни было число С, лежащее между А и B, найдется такая точка x = с между a и b, что
, то каково бы ни было число С, лежащее между А и B, найдется такая точка x = с между a и b, что 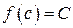 .
.
1 Пусть функция 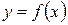 определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке X. Тогда в соответствующем промежутке Y значений этой функции существует однозначная обратная функция
определена, монотонно возрастает (убывает) и непрерывна в некотором промежутке X. Тогда в соответствующем промежутке Y значений этой функции существует однозначная обратная функция 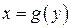 , также монотонно возрастающая (убывающая) и непрерывная.
, также монотонно возрастающая (убывающая) и непрерывная.
1 Первая теорема Вейершраса. Если функция 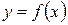 определена и непрерывна в замкнутом промежутке
определена и непрерывна в замкнутом промежутке 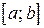 , то она ограничена, т.е. существуют такие константы m и M, что
, то она ограничена, т.е. существуют такие константы m и M, что 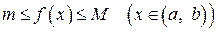 .
.
1 Вторая теорема Вейершраса. Если функция 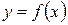 определена и непрерывна в замкнутом промежутке
определена и непрерывна в замкнутом промежутке 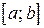 , то она достигает в этом промежутке своего наибольшего и наименьшего значения.
, то она достигает в этом промежутке своего наибольшего и наименьшего значения.
Причем функция достигает в замкнутом промежутке наибольшего и наименьшего значения или в точках локального экстремума или на концах промежутка.
Задача 6.7. Найти наибольшее и наименьшее значение функции 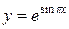 на отрезке [0, 1].
на отрезке [0, 1].
Решение. Определим критические точки данной функции. Для этого приравняем к нулю ее первую производную:
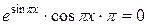 .
.
Очевидно, что решениями полученного уравнения являются числа 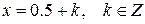 . Только один корень
. Только один корень 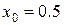 принадлежит рассматриваемому интервалу [0, 1]. Для нахождения наибольшего и наименьшего значения функции
принадлежит рассматриваемому интервалу [0, 1]. Для нахождения наибольшего и наименьшего значения функции 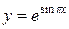 на отрезке [0, 1] достаточно сравнить значение функции в критической точке (не выясняя при этом, есть ли в данной точке экстремум) с ее значениями на концах отрезка:
на отрезке [0, 1] достаточно сравнить значение функции в критической точке (не выясняя при этом, есть ли в данной точке экстремум) с ее значениями на концах отрезка:
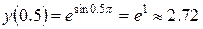 ,
, 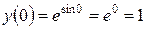 ,
, 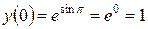 .
.
Таким образом, наибольшее значение функции 2,72 достигается в точке 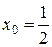 , наименьшее значение функции 1 достигается в двух точках
, наименьшее значение функции 1 достигается в двух точках 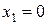 и
и 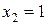 .
.
Глава 7. Неопределенный интеграл
 2015-04-01
2015-04-01 787
787








