Предположим, что на некотором интервале 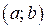 определена непрерывная функция
определена непрерывная функция 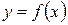 .
.
2Первообразной функции 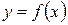 на интервале
на интервале 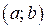 называется функция
называется функция 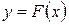 такая, что
такая, что 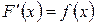 при любом
при любом 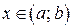 .
.
g Теорема (об общем виде всех первообразных). Первообразная функции 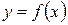 определяется с точностью до константы, а точнее выполняются два утверждения:
определяется с точностью до константы, а точнее выполняются два утверждения:
1) если функция 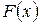 является первообразной функции
является первообразной функции 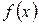 на некотором интервале
на некотором интервале 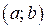 , то функция
, то функция 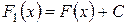 также является первообразной функции
также является первообразной функции 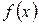 на данном интервале для любой константы С;
на данном интервале для любой константы С;
2) если 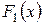 и
и 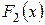 – две первообразные функции
– две первообразные функции 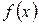 на интервале
на интервале 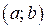 , то их разность является константой:
, то их разность является константой:
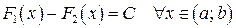 .
.
4 1) Найдем производную функции 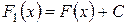 :
:
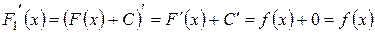
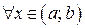 .
.
Таким образом, функция 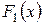 является первообразной функции
является первообразной функции 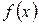 на интервале
на интервале 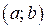 .
.
2) Найдем производную функции 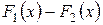 :
:
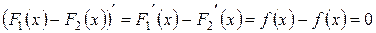 . По следствию из теоремы Лагранжа (гл. 6) отсюда вытекает, что
. По следствию из теоремы Лагранжа (гл. 6) отсюда вытекает, что 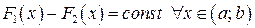 .3
.3
2 Множество всех первообразных функции 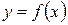 на некотором интервале
на некотором интервале 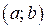 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции 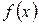 и обозначается
и обозначается 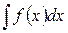 . Функция f (x) называется подынтегральной функцией.
. Функция f (x) называется подынтегральной функцией.
Таким образом, 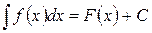 , где
, где 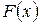 – одна из первообразных функции
– одна из первообразных функции 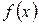 .
.
2 Функция 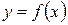 , имеющая хотя бы одну первообразную на интервале
, имеющая хотя бы одну первообразную на интервале 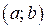 , называется функцией, интегрируемой на интервале
, называется функцией, интегрируемой на интервале 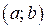 .
.
1 Интегрирование и дифференцирование являются взаимно-обратными операциями, в том смысле, что
1) 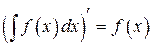 ; 2)
; 2) 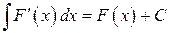 .
.
(данные свойства проверяются непосредственно).
2 Два интеграла называются равными на некотором интервале 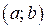
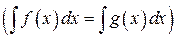 , если первообразные обеих подынтегральных функций
, если первообразные обеих подынтегральных функций 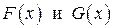 соответственно, отличаются не более, чем на константу:
соответственно, отличаются не более, чем на константу: 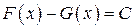 ,
, 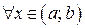 .
.
Интегралы от наиболее распространенных функций приведены в следующей таблице:
Таблица интегралов
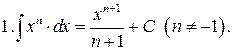
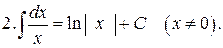
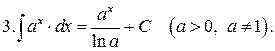
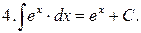
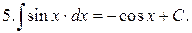
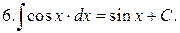
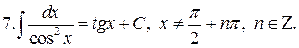
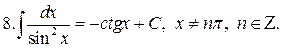
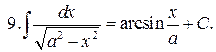
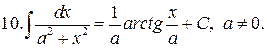
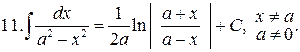
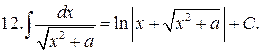
Формула (12) справедлива при всех x, удовлетворяющих неравенству 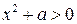 .
.
Все табличные формулы справедливы только при тех значениях переменной x, которые входят в область определения подынтегральной функции. Каждую из этих формул можно доказать с помощью дифференцирования. Докажем некоторые из них:
g 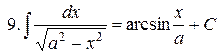 .
.
4Найдем производную
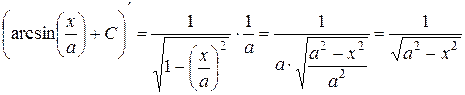 . Мы получили подынтегральную функцию. Отметим, что формула (9) справедлива только при тех значениях x, при которых
. Мы получили подынтегральную функцию. Отметим, что формула (9) справедлива только при тех значениях x, при которых 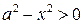 , т.е. при
, т.е. при 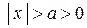 .3
.3
g 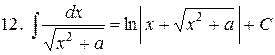 .
.
41) Найдем производную функции 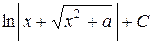 в том случае, когда выражение
в том случае, когда выражение 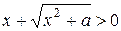 :
:
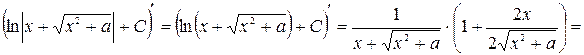
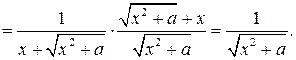
2) Пусть теперь 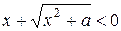 . Тогда:
. Тогда:
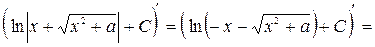
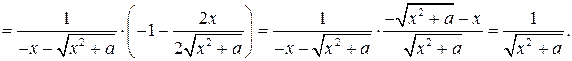
В обоих случаях мы получили подынтегральную функцию. 3
 2015-04-01
2015-04-01 811
811








