2015-04-01
325
1. g Пусть функция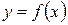 
, является интегрируемой на интервале 
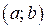и a – некоторая константа, отличная от нуля. Тогда постоянный множитель можно выносить за знак интеграла:
, 
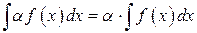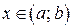(7.1)
4 Обозначим через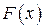 
– одну из первообразных функции 
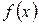на интервале 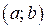. Тогда 
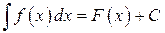и
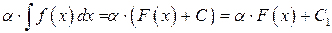, (7.2)
где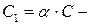 
произвольная константа.
Очевидно, что функция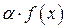 
является интегрируемой на интервале 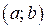, и в качестве одной из ее первообразных можно взять функцию 
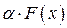. Действительно,
.
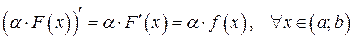Следовательно,
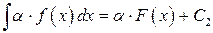, (7.3)
где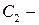 
произвольная константа. Сравнивая равенства (7.2) и (7.3), мы приходим к выводу, о равенстве интегралов:
, 
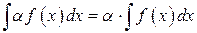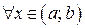. 3
2. g Пусть функции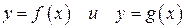 
интегрируемы на интервале 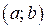. Тогда на интервале 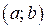интеграл от суммы данных функций равен сумме интегралов:
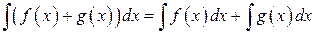(7.4)
4 Обозначим через 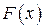– произвольную первообразную функции 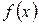, а через 
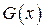– произвольную первообразную функции 
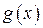на интервале 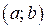. Тогда 
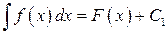и 
. Т.е.
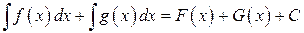, (7.4)
где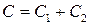 
Очевидно, что функия 
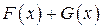является первообразной суммы 
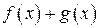. Действительно,
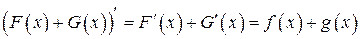. Следовательно,
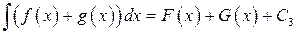(7.5)
Сравнивая равенства (7.4) и (7.5), мы убеждаемся в том, что
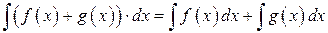. 3
