1. Упрощающие постановки. Выбирая в структуре подынтегральной функции некоторое выражение и обозначая его новой переменной, иногда удается существенно упростить интеграл (и даже свести его к табличному).
Пример 7.5. Найти неопределенный интеграл 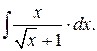
Произведем замену переменной 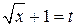 . Тогда
. Тогда
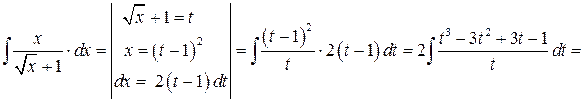
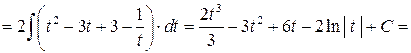
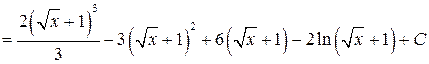 .
.
Дальнейшие упрощения, связанные с раскрытием скобок и приведением подобных членов, предоставляем читателям.
Задача 7.6. Найти интеграл 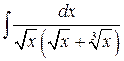 .
.
Решение. Произведем замену 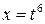 . При этом
. При этом 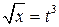 ,
, 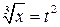 :
:
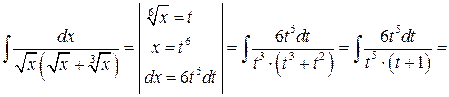
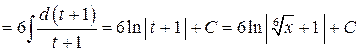 .
.
2. Тригонометрические подстановки. В интегралах вида
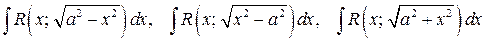 от квадратного корня можно избавиться с помощью замены
от квадратного корня можно избавиться с помощью замены 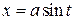 ,
, 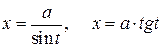 соответственно (через R обозначена рациональная функция).
соответственно (через R обозначена рациональная функция).
Пример 7.7. Найти интеграл 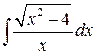 .
.
В данном случае а 2 = 4 (а = 2) и, следовательно, мы производим замену 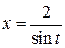 :
:
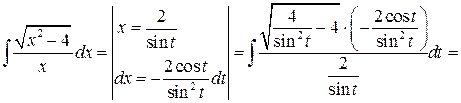
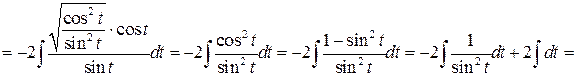
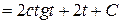 .
.
 2015-04-01
2015-04-01 864
864








