Подведение множителя под знак дифференциала

Преобразование 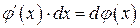называется подведением множителя под знак дифференциала. Используя данное преобразование, интегралы вида 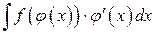можно преобразовать следующим образом:

,

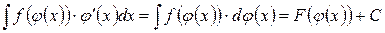где 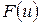– первообразная функции .

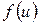Пример 7.3. Найти неопределенный интеграл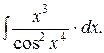

Умножим и разделим подынтегральную функцию на 4 и внесем множитель 4 x ³ под знак дифференциала:

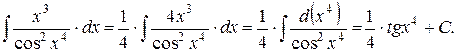
Для того чтобы под знаком дифференциала получить линейную функцию, достаточно воспользоваться очевидным равенством:

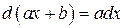или .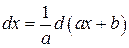

Постоянный множитель 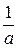можно при этом вынести за знак интеграла.

Пример 7.4. Найти неопределенный интеграл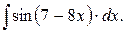

Умножим и разделим подынтегральную функцию на –8 и внесем множитель –8 под знак дифференциала: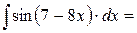

.

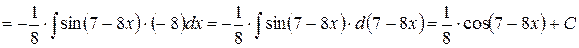Познакомимся с двумя основными методами нахождения неопределенных интегралов – заменой переменной и интегрированием по частям.