2015-04-01
727
Глава 10. ПРОСТЕЙШИЕ Дифференциальные уравнения
2 Дифференциальным уравнением называется уравнение вида
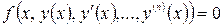, (10.1)
где x – независимая переменная, y (x) – неизвестная функция y ( i )(x) – производная функции y (x) i -го порядка. Порядок старшей производной, входящей в уравнение (10.1), называется порядком дифференциального уравнения.
2 Функция y (x), обращающая дифференциальное уравнение (10.1) в тождество, называется решением дифференциального уравнения. Как правило, дифференциальное уравнение имеет бесчисленное множество решений. Множество всех решений уравнения (10.1) называют общим решением дифференциального уравнения. Конкретный представитель общего решения (обычно удовлетворяющий какому-нибудь дополнительному требованию) называют частным решением дифференциального уравнения. Общее или частное решение дифференциального уравнения, полученное в виде неявной функции, называют соответственно общим или частным интегралом дифференциального уравнения.
С простейшими дифференциальными уравнениями вида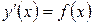 
мы сталкивались, решая задачу интегрирования функции.
Пример 10.1. Найти общее решение дифференциального уравнения: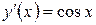 
.
Очевидно, что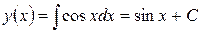 
– общее решение дифференциального уравнения; 
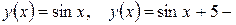некоторые частные решения.
