Ведем обозначения 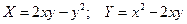 .
.
Для того, чтобы выражение (1) было полным дифференциалом функции 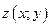 необходимо и достаточно выполнение условия:
необходимо и достаточно выполнение условия: 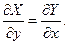
Найдем 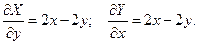 Следовательно, выражение (1) есть полный дифференциал. Полный дифференциал выражается формулой:
Следовательно, выражение (1) есть полный дифференциал. Полный дифференциал выражается формулой: 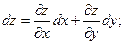
где 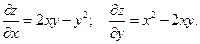
Интегрируя первое равенство по 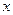 , находим искомую функцию
, находим искомую функцию 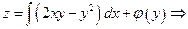
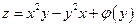 .
.
Тогда частная производная от z по у:
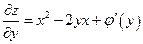 .
.
Но из условия 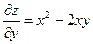
Найдем 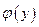 из уравнения
из уравнения 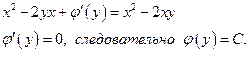
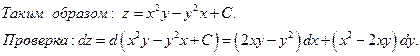
Задание 4.
Заменив приращение функции дифференциалом, приближенно вычислить 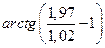 .
.
 2015-04-17
2015-04-17 711
711








