Решение. Логарифм определен только при положительном значении его аргумента, поэтому

Логарифм определен только при положительном значении его аргумента, поэтому

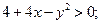или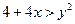

Чтобы изобразить геометрически область D, найдем сначала ее границу:

.

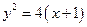Полученное уравнение определяет параболу, вершина которой расположена в точке 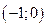, а ось направлена в положительную сторону оси Ох.

Точки пересечения параболы с осью Оу получаются из условия

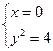
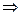(0; 2), (0; -2).

Парабола делит всю плоскость на две части – внутреннюю и внешнюю по отношению к параболе. Для точек одной их этих частей выполняется неравенство 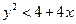, а для другой 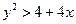(на самой параболе 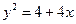). Чтобы установить, какая из этих двух частей является областью определения данной функции, т.е. удовлетворяет условию 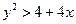, достаточно проверить это условие для какой-нибудь одной точки, не лежащей на параболе. Например, начало координат О (0; 0) лежит внутри параболы и удовлетворяет нужному условию: 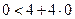. Следовательно, рассматриваемая область D состоит из внутренних точек плоскости относительно параболы. Сама парабола в область D не входит.

Графическое изображение области определения функции.