С помощью критерия Розенбаума

“Знание основ программирования”	“Интеллект”
	Д	Ю			Д	Ю
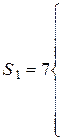
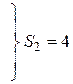
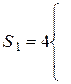
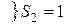
Суммы:				Суммы:
Средние:	10,15	14,18	Средние:	27,08	30,18

Эмпирическое значение 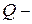критерия Розенбаума равно

.

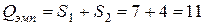По таблице критических значений 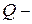критерия Розенбаума [2, 3] найдем:

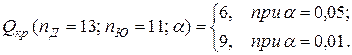
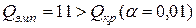, следовательно, гипотеза 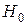(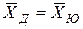) об отсутствии различий в уровне исследуемого признака двух независимых выборок против альтернативы 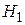(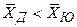) о существовании статистически значимых различий в уровне признака может быть отвергнута при .

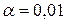Таким образом, с уверенностью 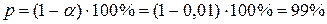можно сделать вывод о том, что данные исследования не противоречат гипотезе 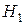: юноши статистически значимо превосходят девушек по знаниям основ программирования.

2.в) Сравнение уровней интеллекта юношей и девушек с помощью критерия Розенбаума (табл. 3.4).

Из полученных расчетов, видно, что выборочное среднее значение уровня интеллекта у девушек (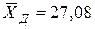) ниже, чем у юношей ().

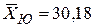Сформулируем статистические гипотезы.

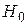: различие юношей и девушек по уровню интеллекта статистически незначимо (формально: );

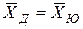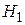: юноши статистически значимо превосходят девушек по уровню интеллекта (формально: ).

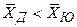Упорядочим показатель интеллекта юношей и девушек (табл. 3.4).

Определим самое низкое значение в выборке юношей (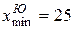) и подсчитаем S₁ - количество 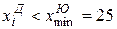: S₁ = 4. Аналогично, определим самое высокое значение в выборке девушек (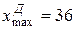) и подсчитаем S₂ - количество 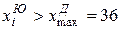: S₂ = 1.

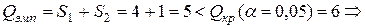, принимается гипотеза 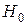об отсутствии значимых различий в уровне интеллекта юношей и девушек.

Общий вывод по второму вопросу исследования: юноши и девушки не различаются по успешности обучения (на МФ КемГУ) и по общему уровню интеллектуального развития, и с доверительной вероятность 99% можно утверждать о том, что юноши проявляют более высокие способности к программированию, чем девушки.

3) Для ответа на третий вопрос исследования – Существует ли какая-либо связь между измеренными показателями? - необходимо, прежде всего, правильно подобрать подходящий коэффициент связи, затем рассчитать его значение, оценить статистическую значимость отличия коэффициента связи от нуля (установить факт наличия связи) и проинтерпретировать полученные результаты.

3.а) Для исследования корреляции между порядковым признаком “успешность обучения” и количественным признаком “знание программирования” можно воспользоваться коэффициентом ранговой корреляции Спирмена 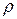[1]:

,

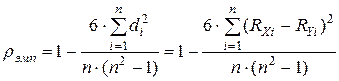где 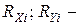ранги 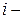ых значений двух исследуемых признаков 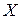и .

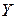Таким образом, для расчета коэффициента Спирмена 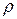необходимо, предварительно, проранжировать последовательности наблюдений признаков “успешность обучения” (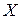) и “знание программирования” (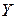) (см. табл. 3.5).

Таблица 3.5