Расчет коэффициента Пирсона

для признаков “знание основ программирования” и “уровень IQ”

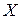
Студент (№ п/п)	Знание программирования,	Уровень IQ,
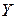
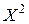
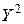
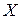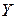
Суммы:

Критические значения коэффициента Пирсона 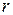в зависимости от объема выборки 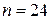и уровня значимости 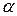равны [1, 3]:

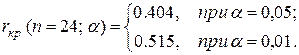
Так как 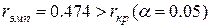, то гипотеза 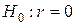(связи нет) отвергается при 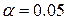, и с доверительной вероятностью 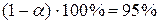может быть принята альтернативная гипотеза : .

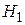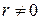Таким образом, с уверенностью 95% можно говорить о существовании прямой (т.к. 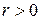) линейной связи между знанием основ программирования и уровнем интеллекта у студентов МФ. Детерминация данной связи равна 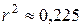, поэтому лишь на 22,5% знание основ программирования зависит от уровня интеллекта, и на 77,5% от других факторов, т.е. данную связь по тесноте можно охарактеризовать как слабую [1].

Общий вывод по третьему вопросу исследования.

У студентов МФ КемГУ отделения “Прикладной математики” выявляется статистически значимая (при 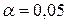), прямая, но слабая связь знаний основ программирования с успешностью обучения на МФ (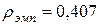) и с уровнем интеллекта (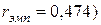). Статистически значимой связи между успешностью обучения на МФ и с уровнем интеллекта не проявляется ().

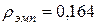ЛИТЕРАТУРА

1. Каган Е.С., Морозова И.С., Невзорова Т.А. Выявление взаимосвязей в психологических исследованиях: Учебное пособие. – Кемерово, КемГУ, 2002. – 81 с.

2. Каган Е.С. Применение методов теории статистического вывода в психологических исследованиях: Учебное пособие. – Кемерово, Кузбассвузиздат, 2005. – 113 с.

3. Таблицы математической статистики: Учебно-методическое пособие. - Кемерово, Кузбассвузиздат, 2006. – 48 с.

* Напомним, что критерий Манна – Уитни является одним из исключений из общего правила принятия решения о достоверности различий, а именно гипотеза отвергается, если.

* Тесты IQ свидетельствуют об общем уровне интеллектуального развития, в которых индивиду предлагается ряд заданий, подобранных таким образом, чтобы была обеспечена адекватная выборка и оценка всех важнейших интеллектуальных функций. Краткий ориентировочный тест (КОТ) является адаптацией теста IQ Вандерлика для русскоязычных респондентов.

* Для статистического подтверждения предположения о нормальном законе распределения признака в данном исследовании слишком мал объем наблюдений:, а для достоверности выводов необходимо иметь.

* Несмотря на распространенную практику отношения к оценкам как к количественным данным, шкала оценок (баллов): 2, 3, 4, 5 – является порядковой (ранговой) шкалой, т.к. оценка характеризует лишь принадлежность к тому или иному упорядоченному классу: “неудовлетворительные”, “удовлетворительные”, “хорошие” и “отличные” знания и не несет информации на сколько и/или во сколько раз одна оценка лучше или хуже другой.

В связи с этим при обработке и анализе данных, измеренных в оценках 2, 3, 4 5, наиболее корректным будет применение процедур и методов, предназначенных для ранговых шкал.