Критерий Михайлова

В 1938 году советским ученым А.В.Михайловым (в 23года был награжден премией Ленинского комсомола) был предложен графоаналитический критерий устойчивости, названный в его честь. Данный критерий позволяет не только судить об устойчивости, но и наглядно оценивать степень влияния параметров системы на ее устойчивость.

Рассмотрим основные положения критерия Михайлова. Пусть характеристический полином системы D(p) имеет вид:

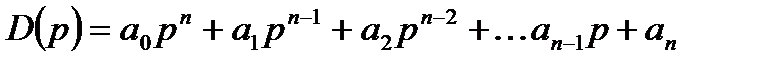(21.14)

Предположив, что корни нам известны, воспользуемся теоремой Виета.

Тогда выражение (21.14) запишется как:

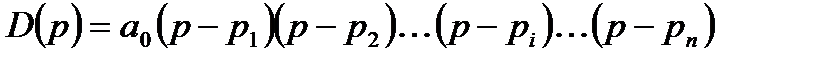, (21.15)

где 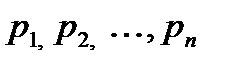–корни характеристического уравнения.

Рассмотрим один из сомножителей: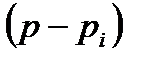

Воспользуемся комплексной плоскостью (рис.21.3). Пусть 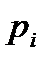- вещественный отрицательный корень .

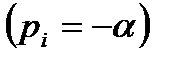а б j

j

(р-р_i) (р-р_i^⃰ )

p=jω

p_i 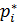p_i 0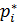

Рис.21.3. К пояснению критерия Михайлова

Тогда на этой плоскости корень p_i изобразиться в виде вектора. Поскольку р независимая переменная, можно задать любое ее значение. В том, каким выбрать вектор р, и заключается догадка Михайлова. Необходимо было выбрать вектор р, чтобы вектор (p-p_i) каким-то образом отразил бы тот факт, что корень р_i лежит в левой, а не в правой полуплоскости. На первый взгляд, кажется целесообразным выбрать для этого нечто среднее на границе между левой и правой полуплоскостями. Михайлов выбирает вектор р "посередине": 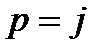w. Тогда вектор (р-р_i.) расположен так, как показано на рис. I3,б. Для 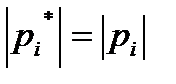имеем другой вектор 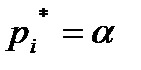, расположенный в правой полуплоскости. Следующая догадка Михайлова заключалась в том, чтобы менять величину w и рассматривать вектор (р-р_i) "в движении". Пусть ω меняется от 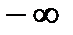до 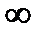, тогда вектор (р-р_i) будет поворачиваться по часовой стрелке, а вектор 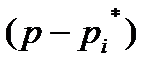против часовой стрелки. Причем, для первого поворот составит +p, а для второго - p радиан, считая, как принято, за положительное направление - движение против часовой стрелки.

Формализуем установленные факты. Заменив в (21.15) р на 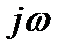, получим

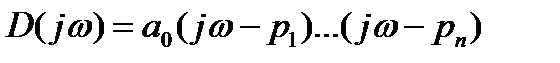(21.16)

Каждый из сомножителей (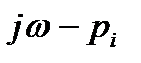) представляет собой комплексное выражение и может быть представлен в показательной форме записи:

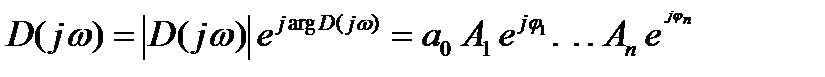. (21.17)

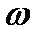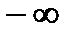При изменении от до 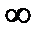для случая, когда все корни лежат в левой полуплоскости, будем иметь

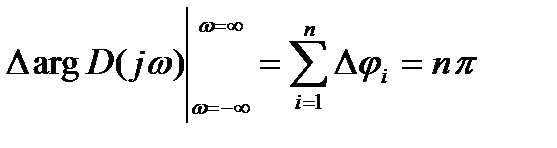. (21.18)

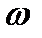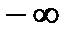Отсюда можно сформулировать критерий Михайлова следующим образом: для того, чтобы АСР, имеющая характеристическое уравнение n - го порядка, была устойчива, необходимо и достаточно, чтобы при изменении от до 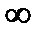изменение аргумента вектора 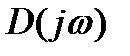было равно np.

В этом случае, когда характеристическое уравнение системы содержит из n корней m корней с положительной вещественной частью, это найдет отражение в 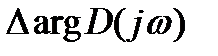, которое будет меньшим, чем np

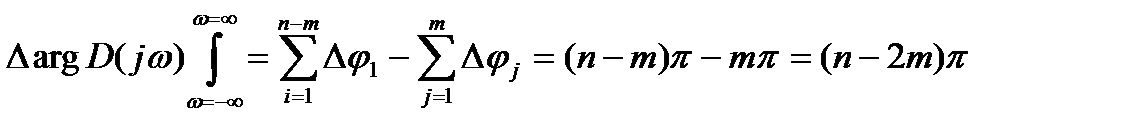(21.19)

На практике использование критерия Михайлова сводится к следующим шагам:

I.Записывается характеристический многочлен системы

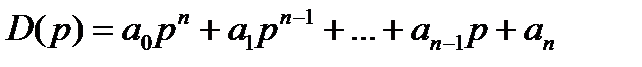
2. p заменяется на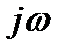

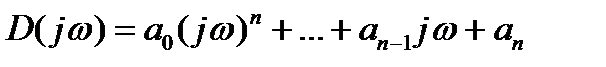
З.На комплексной плоскости строится вектор 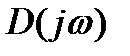для различных значений 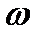>0.

Замечание:

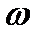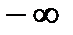при изменении от до 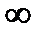представляет собой симметричную относительно оси абсцисс кривую. Поэтому для уменьшения трудоемкости построений и расчетов рассматривают лишь одну ветвь для 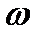>0, меняющихся от 0 до 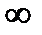.При этом выражение (21.12) используется в виде

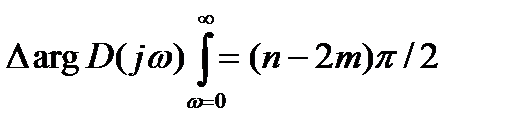(21.20)

4. Соединяя полученные при различных 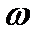точки на комплексной плоскости плавной кривой, получается так называемый годограф Михайлова.

Примеры годографов для систем показаны на рис.21.4.

Кривая I на рис.21.4в соответствует наличию мнимых корней или, как говорят, колебательной границе устойчивости, а кривая 2 (пунктирные линии)- наличию вещественного нулевого корня- апериодической границе устойчивости. Как следует из рассмотрения рис. 21.4и формулы (21.19) у устойчивых систем _;годограф Михайлова последовательно пересекает а квадрантов, что и служит правилом для суждения об устойчивости.

При изменении параметров систем годограф Михайлова деформируется. При этом меняется его расположение относительно системы координат, что само по себе говорит о степени влияния изменения того или иного параметра на устойчивость. Последнее обстоятельство становится особенно важным при решении задач проектирования систем.

jV n=1 jV jV 2

n=2 n=5

U n=4 U U

n=3 n=4

а б в

Рис.21.4. Примеры: а - устойчивых, б - неустойчивых АСР и в - АСР, находящихся на границах устойчивости: колебательной -1 и апериодической -2 границах устойчивости.