Критерий Найквиста

Рассмотрим передаточную функцию системы с обратной связью (замк­нутой системы):

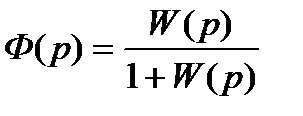(21.21)

Из выражения (21.5.1) видно, что между Ф(р) и W(p) существует взаимно-однозначное соответствие. Это значит, что особенности W(p) однозначно отражаются в особенностях Ф(р) и наоборот. Однако выражение W(p) проще, чем Ф(р). Это объясняет тот факт, что при решении задач анализа и синтеза АСР стремятся используемые методы исследования и расчета замкнутых систем свести к оперированию с W(P) т.е. с их передаточной функцией в разомкнутом состоянии, а по полученным результатам сделать заключение о Ф(р), т.е. о свойствах замкнутых систем.

Сказанное относится к критерию Найквиста, основанному на критерии Михайлова. Так, если по критерию Михайлова за основу берется характеристическое уравнение замкнутой системы (21.14), то по критерию Найквиста для суждения об устойчивости замкнутой системы рассматривается передаточная функция W(p).

Для вывода критерия Найквиста возьмем общий случай, когда объект управления неустойчив, а за счет введения обратной связи и регулятора, удается сделать его устойчивым.

Пусть имеем

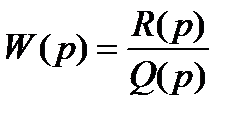(21.22)

где R(p) -полином степени m, а Q(р)-характеристический полином разомкнутой системы степени n

Тогда

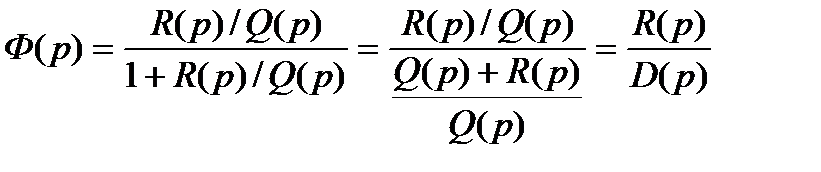, (21.23)

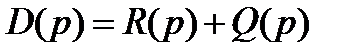-характеристический полином замкнутой системе степени n. Пусть в соответствии с рассматриваемым случаем Q(p) имеет l корней с положительной вещественной частью и следовательно (n- l) корней с отрицательной вещественной частью, а 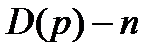корней с отрицательной вещественной частью. Установим какое поведение годографа W (jw) будет этому соответствовать.

По критерию Михайлова имеем

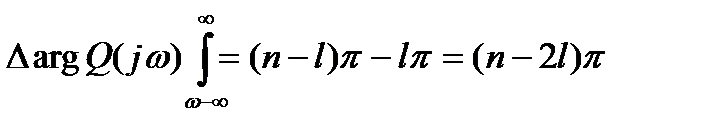(21.24)

Тогда 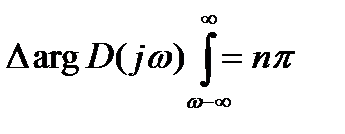(21.25)

Рассматривая поведение вектора 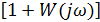на комплексной плоскости (рис. 21.15,а).

Cделаем заключение о поведении вектора W(jω).Так как W(jω) является составляющим вектора 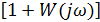, тo для его отдельного рассмотрения введем новую систему координат с центром в 0^′. Проследим за концом вектора W(jω) по рис. 21.15,б. Из рисунка следует, что при изменении ω вектор W(jω) охватывает точку с координатами (-1, j0).

На основании отмеченного сформулируем критерий Найквиста: если разомкнутая система неустойчива, то для устойчивой в замкнутом состоянии системы амплитудно-фазовая частотная характеристика разомкнутой системы при изменении ω от -∞ до ∞ охватывает точку с координатами (-1,j0) l раз, где l - число корней характеристического уравнения разомкнутой системы с положительной вещественной частью.

а б

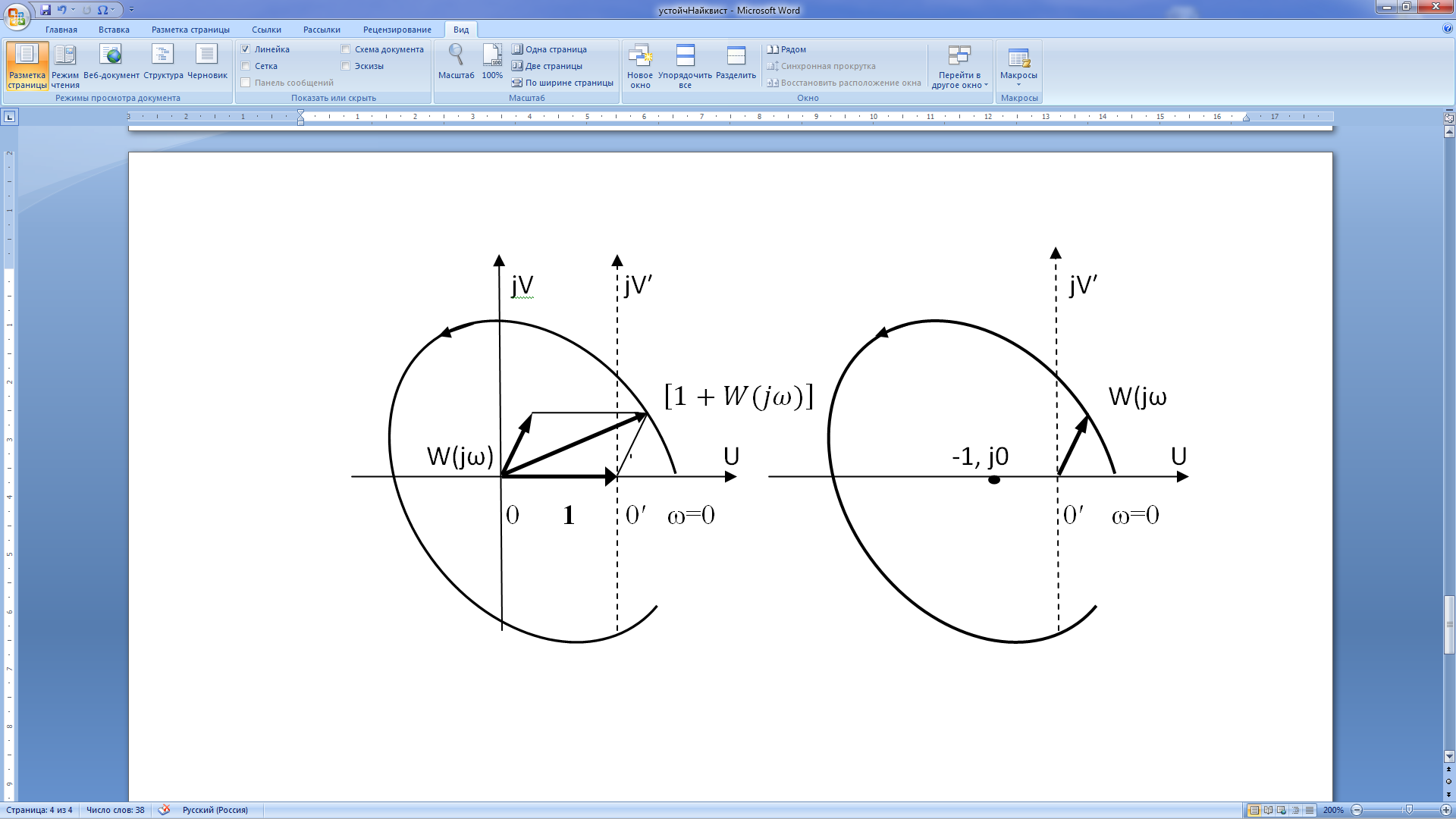
Рис.21.5. Пояснения к критерию Найквиста

При l =0 устойчивая система имеет АФЧХ разомкнутой системы, не охватывающую точку с координатами (-1, j0). Если же устойчивая в разомкнутом состоянии система при введении обратной связи стала неустойчивой, об этом можно судить по тому, что АФЧХ разомкнутой системы охватывает точку с координатами (-1, j0).

Здесь уместно еще раз повторить: за счет управления можно даже неустойчивый объект сделать устойчивым, в то время как при плохо выбранном законе регулирования можно даже устойчивый сам по себе объект сделать неустойчивым в управлении.

Таким образом, критерий Найквиста на основании W(jω) даёт возможность судить о правильности выбора параметров систем с точки зрения их устойчивости.

При построении АФЧХ для W(jω) достаточно построить одну ветвь при ω от 0 до - ∞, так как другая (при W от 0 до -∞) является симметричной первой относительно оси абсцисс.

Сложность возникает, когда характеристическое уравнение разомкнутой системы Q (p)=0 имеет корни на границе устойчивости, т.е. с нулевой вещественной частью.

В качестве примера возьмём систему с передаточной функцией

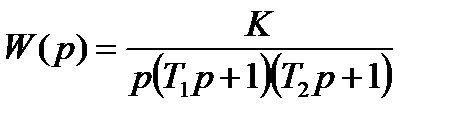. (21.26)

Соответствующая частотная передаточная функция будет равна

W(jw)=A(ω) 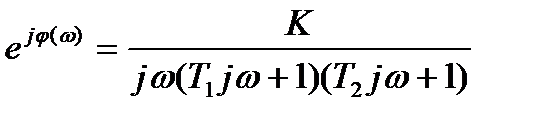, (21.27)

где

A(ω)= 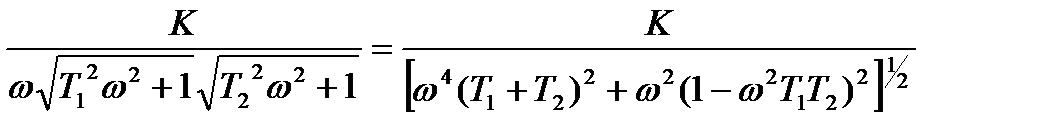, (21.28)

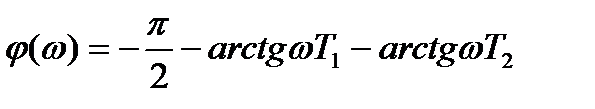. (21.29)

Построим АФЧХ для ω>0, при ω=0⁺ получаем А (0⁺)=∞ и φ(0⁺)=-90^о. При ω→∞ будем иметь lim A (ω) =0 и φ(∞)=-270^о. Для ω<0 АФЧХ будет симметрична кривой, полученной при ω>0 (рис.21.6,б). Для разрешения неопределённости, возникающей при ω=0 для нулевого корня р=0, нулевые корни причислять к отрицательным корням с бесконечной малой отрицательной частью (рис. 21. 6, а). Этому соответствует замыкания АФЧХ при ω от 0^- к 0⁺ по часовой стрелке, по окружности бесконечно большого радиуса, как показано на рис. 21.6, б. В данном случае система неустойчива, так как годограф охватывает точку (-1, j0) 2 раза.

Следовательно, число корней в правой полуплоскости равно 2. Точка пересечения годографа с вещественной осью может быть найдена из уравнения

, (21.30)

которое справедливо при 1 – ω² T₁ T₂ =0 или ω=1/ 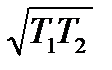. Величина
ReW (jω)=U (ω) при этой частоте будет

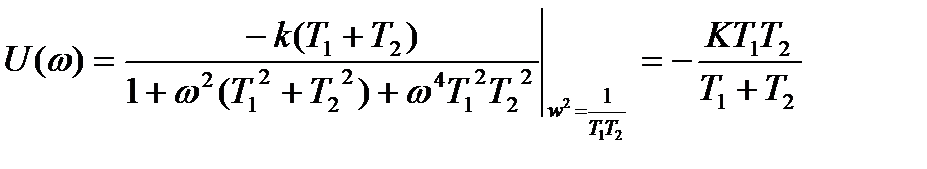. (21.31)

а б в

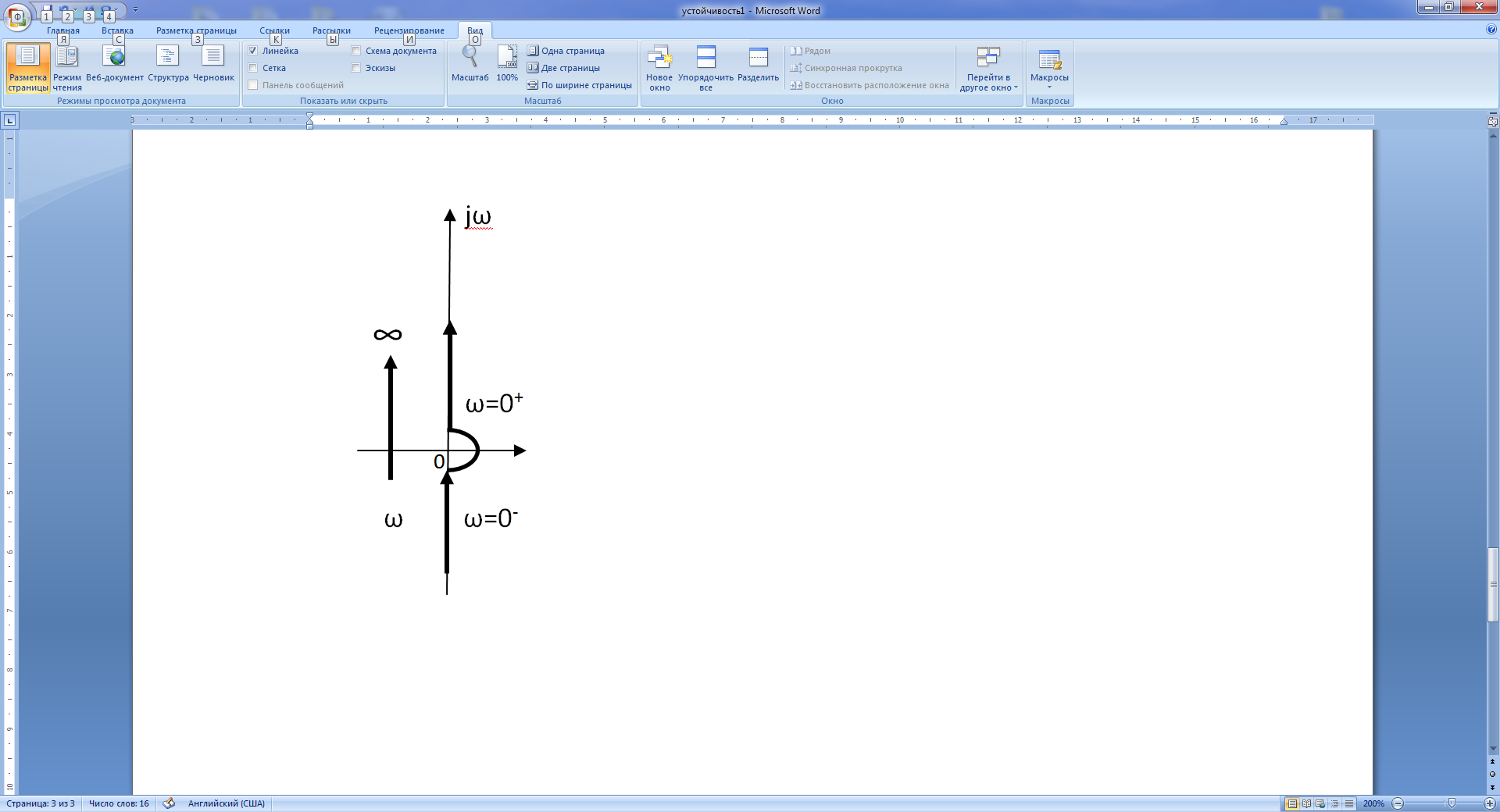
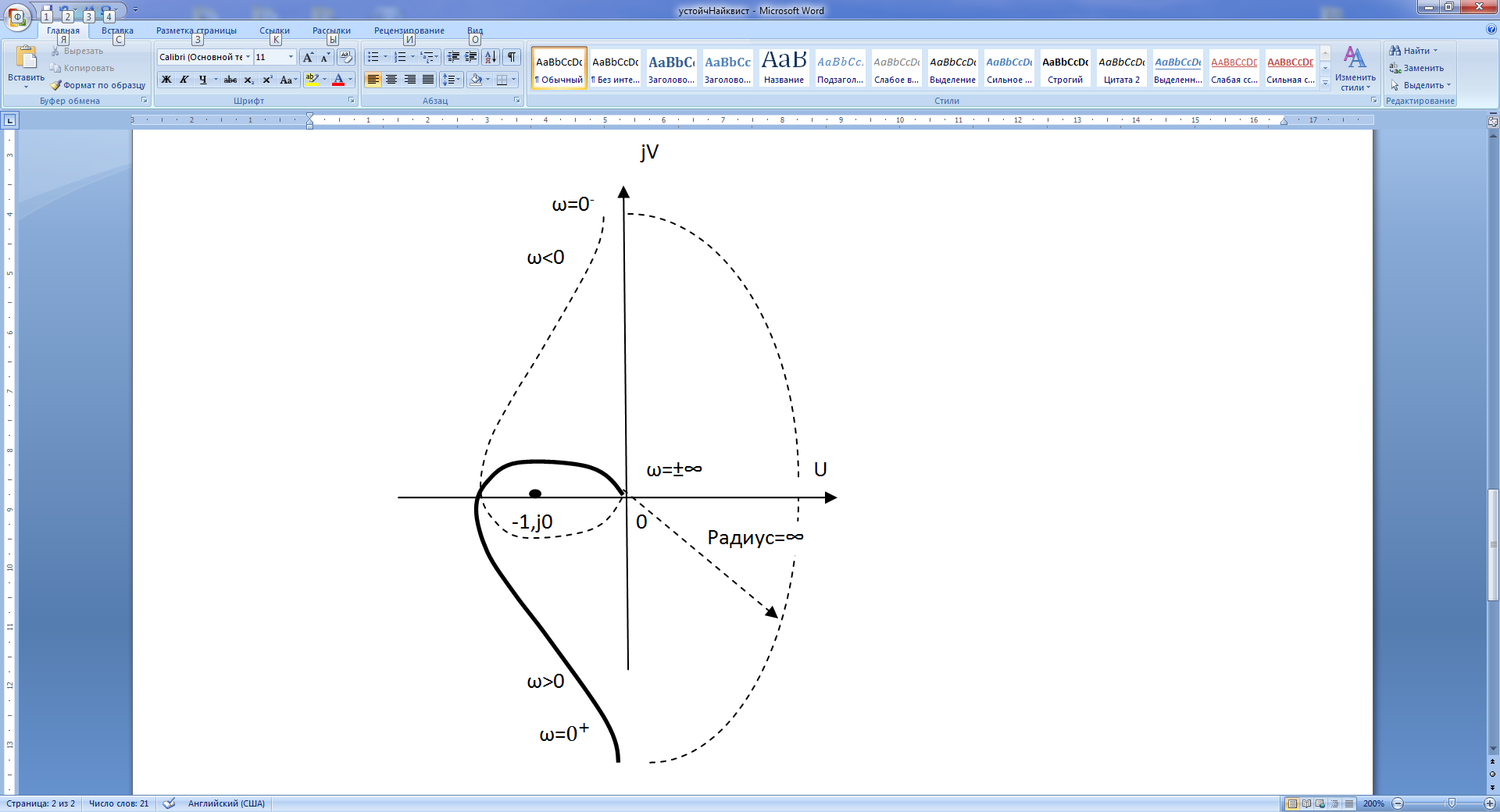
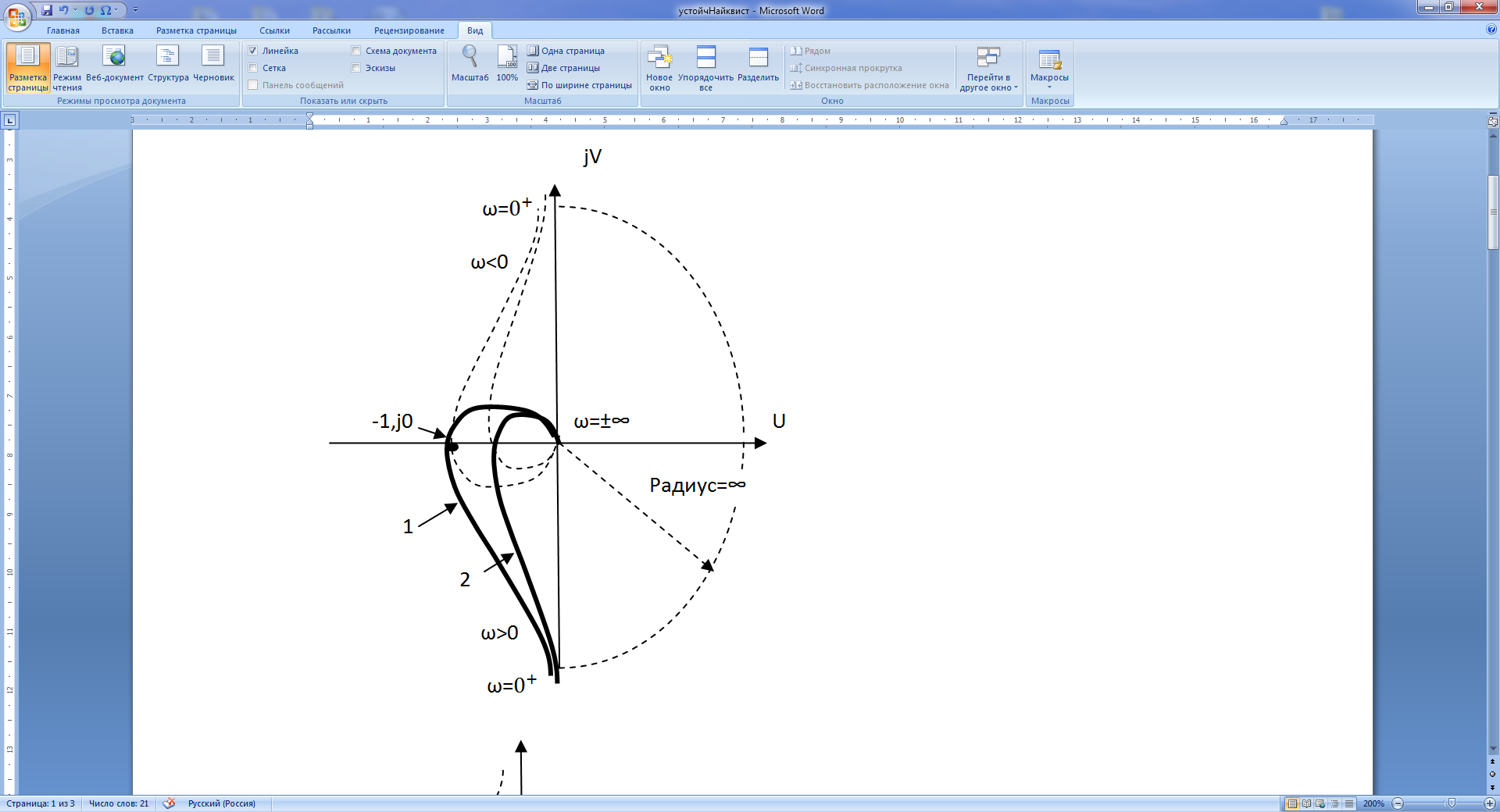
Рис. 21.6. а – изменение аргумента ω; б, в – годографы систем.

Отсюда систему можно сделать устойчивой, когда

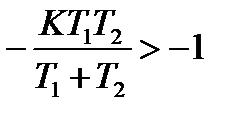, т. е. при 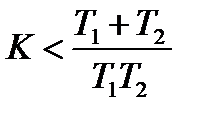. (21.32)

В том случае, когда , система будет находиться на границе устойчивости, а годограф проходит проходит через точку (-1; j0).

На рис. 21.6 показан случай неустойчивости системы – б, системы, находящейся на границе устойчивости (в, годограф 1), и устойчивой системы (в, годограф 2).