Расчет на прочность по безмоментной теории: уравнение Лапласа, уравнение зоны

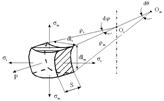
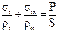уравнение Лапласа. Одного этого уравнения недостаточно для определения напряжений s_m и s_t

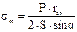уравнением зоны.

Из этого уравнения находится меридиональное напряжение s_m.

Таким образом, по безмоментной теории напряжения s_m и s_t в оболочке определяются из уравнений равновесия.

15. Напряжения возникающие в стенках оболочек. Вывод,напряжений и толщины стенки цилиндрической обечайки

– цилиндр с крышками, нагруженный равномерно распределенным давлением Р.

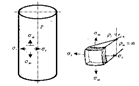Для него r_t = R, r_m =¥, тогда

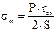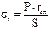, ,при этом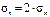

то есть в продольных швах действуют в два раза большие напряжения, чем в поперечных и соответственно по этим швам в первую очередь может произойти разрушении оболочки.

Цилиндрическая оболочка. Толщина стенки определяется на основе третьей теории прочности из следующего выражения ,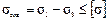

Учитывая, что для цилиндрической оболочк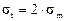и и 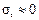, а из курса сопротивления материалов известно, что 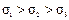принимаем 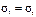; ; 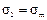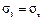_.. Подставив в уравнение (14) значения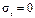

, .

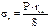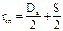Решая его относительно S, получаем следующую формулу для расчета толщины стенки цилиндрической обечайки

. , ,

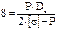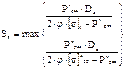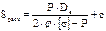16. Напряжения, возникающие в сферических оболочках

Мембранная теория – сферический сосуд (шаровая оболочка, полушаровое днище) нагруженный равномерно распределенным внутренним давлением Р. Для него r_t = r_m = R, где R – радиус сферы.

Тогда меридиональное напряжение s_m равно кольцевому напряжению s_t и они определяются по формуле

,

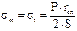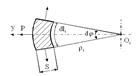
– конус, шарнирно подвешенный по краю со стороны основания, нагруженный равномерно распределенным давлением Р.

Для него r_m = ¥.Кольцевые напряжения в любом сечении конического днища n - n можно найти из уравнения Лапласа.

Учитывая, что величина

, .

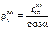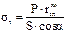где 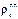, 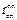– соответственно радиус кривизны и радиус конуса в сечении n – n. Величину меридиональных напряжений, возникающих в сечении n – n конуса можно определить из уравнения зоны (4), т.е 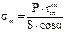. r = R, ,

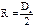при этом кольцевые напряжения (как и для цилиндра) в любом данном сечении в 2 раза больше меридиональных, т.е. .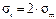

У вершины конуса при г = 0 и кольцевые и меридиональные напряжения равны нулю. Пример эпюры тангенциальных напряжений приведен на рисунке

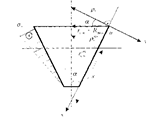
– в эллиптической оболочке

Максимальные напряжения определяются по следующим зависимостям

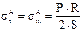,где R - радиус кривизны днища, м, который определяется по формуле 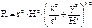, где х и у – координаты заданной точки ри условии, что начало координат находится а точке О;r – радиус днища, м.

В результате экспериментальных исследований было установлено, что оптимальной конструкции днищ соответствуют следующие параметры 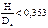. Поэтому стали изготавливать стандартные эллиптические днища с отбортовкой на цилиндр высотой Н и параметрами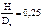

Эллиптические днища одни из самых экономичных. Изготавливаются они штамповкой из листа из круглого проката (если диаметр листа равен диаметру днища, то без сварных швов), либо из сварных листов.