Пример 1: Исследовать функцию на глобальный экстремум 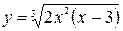 при
при 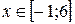 .
.
Решение:
Находим область определения функции и проверяем, содержится ли в ней весь отрезок. 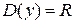 ,
, 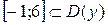 .
.
Определяем все стационарные точки, попадающие в отрезок. Для этого находим производную и приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни.
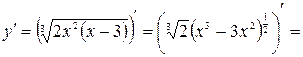
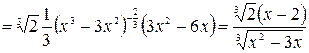 .
.
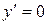 , если
, если 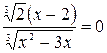 , отсюда
, отсюда
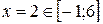
Определяем все критические точки, попадающие в отрезок. Для этого найдем те точки, в которых производная не существует.
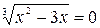
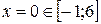 или
или 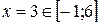 .
.
Вычисляем значение функции в отобранных точках, а также на концах отрезка.
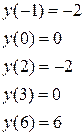
Из полученных значений функции выбираем наибольшее и наименьшее значения.
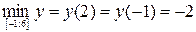 и
и 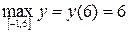 .
.
Ответ: 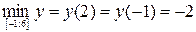 и
и 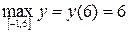 .
.
Пример 2: Найти наибольшее и наименьшее значение функции 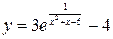 на интервалах
на интервалах
а) 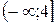 ;
;
б) 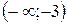 ;
;
в) 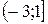 ;
;
г) 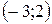 ;
;
д) 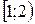 ;
;
е) 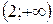 ;
;
ж) 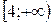 .
.
Решение:
Находим область определения функции и проверяем, содержится ли в ней весь интервал.
Начнем с области определения функции. Квадратный трехчлен в знаменателе дроби не должен обращаться в ноль:
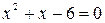
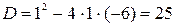
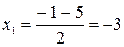
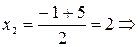
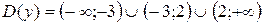 .
.
Легко проверить, что все интервалы из условия задачи принадлежат области определения функции.
Определяем все стационарные точки, попадающие в интервал. Для этого находим производную и приравниваем ее к нулю, решаем полученное уравнение и выбираем подходящие корни.
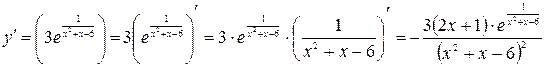
Производная обращается в ноль при 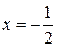 . Эта стационарная точка попадает в интервалы
. Эта стационарная точка попадает в интервалы 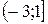 и
и 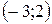 .
.
Определяем все критические точки, попадающие в интервал. Для этого найдем те точки, в которых производная не существует.
Критических точек нет.
Вычисляем значение функции в отобранных точках, а также на концах отрезка в зависимости от вида промежутка.
а) Для первого промежутка 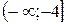 вычисляем значение функции при
вычисляем значение функции при 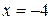 и предел на минус бесконечности:
и предел на минус бесконечности:
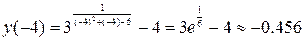
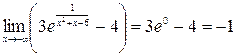
Так как 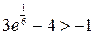 , то
, то 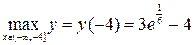 , а о наименьшем значении функции выводов сделать нельзя. Можно лишь утверждать, что значения функции ограничены снизу значением -1 (на минус бесконечности значения функции асимптотически приближаются к бесконечности значения функции асимптотически приближаются к прямой
, а о наименьшем значении функции выводов сделать нельзя. Можно лишь утверждать, что значения функции ограничены снизу значением -1 (на минус бесконечности значения функции асимптотически приближаются к бесконечности значения функции асимптотически приближаются к прямой 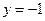 ).
).
б) Второй интервал 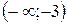 интересен тем, что не содержит ни одной стационарной точки и ни одна из его границ не является строгой. В этом случае мы не сможем найти ни наибольшего, ни наименьшего значения функции. Вычислив предел на минус бесконечности и при стремлении аргумента к –3 слева, мы лишь сможем определить интервал значений функции:
интересен тем, что не содержит ни одной стационарной точки и ни одна из его границ не является строгой. В этом случае мы не сможем найти ни наибольшего, ни наименьшего значения функции. Вычислив предел на минус бесконечности и при стремлении аргумента к –3 слева, мы лишь сможем определить интервал значений функции:
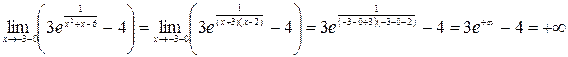
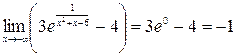
Следовательно, значения функции находятся в интервале 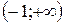 при x из промежутка
при x из промежутка 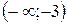 .
.
в) Для третьего промежутка 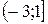 вычислим значении функции в стационарной точке
вычислим значении функции в стационарной точке 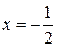 и при
и при 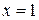 , а также односторонний предел, при стремлении аргумента к -3 справа:
, а также односторонний предел, при стремлении аргумента к -3 справа:
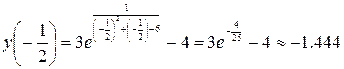
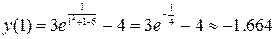
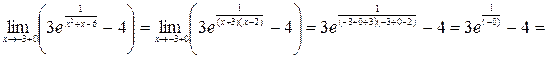
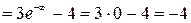 .
.
Следовательно, наибольшее значение на этом интервале функция принимает в стационарной точке 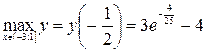 , наименьшее значение функции мы вычислить не можем, но значения функции ограничены снизу величиной -4.
, наименьшее значение функции мы вычислить не можем, но значения функции ограничены снизу величиной -4.
г) Для интервала 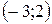 воспользуемся результатами из предыдущего пункта и еще вычислим односторонний предел при стремлении к 2 слева:
воспользуемся результатами из предыдущего пункта и еще вычислим односторонний предел при стремлении к 2 слева:
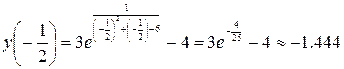
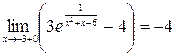
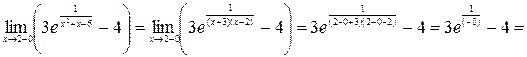
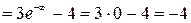 .
.
Поэтому 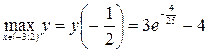 , наименьшее значение определить нет возможности, значения функции ограничены снизу величиной -4.
, наименьшее значение определить нет возможности, значения функции ограничены снизу величиной -4.
д) Результаты предыдущих двух пунктов позволяют утверждать, что на интервале 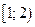 наибольшее значение
наибольшее значение 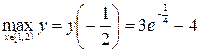 функция принимает при
функция принимает при 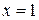 , наименьшее значение найти нельзя, значения функции ограничены снизу величиной -4.
, наименьшее значение найти нельзя, значения функции ограничены снизу величиной -4.
е) На промежутке 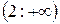 функция не достигает ни наибольшего, ни наименьшего значения.
функция не достигает ни наибольшего, ни наименьшего значения.
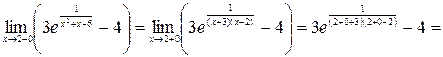
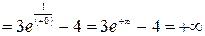 .
.
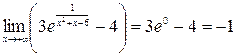
То есть, на этом интервале функция принимает значения из промежутка 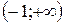 .
.
ж) Вычислив значение функции при 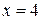 , можно утверждать, что
, можно утверждать, что 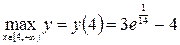 и на плюс бесконечности функция асимптотически приближается к прямой
и на плюс бесконечности функция асимптотически приближается к прямой 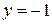 .
.
 2015-04-01
2015-04-01 806
806








