2015-04-01
287
Пусть функция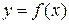 
определена на отрезке 
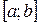. Если 
непрерывна на этом отрезке, то существуют точк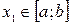и 
и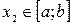 
, в которых функция достигает своего максимального и минимального значений (на отрезке!). Этими точками могут быть либо внутренние критические точки, либо граничные. Поэтому для отыскания наибольшего и наименьшего значения функции на числовом отрезке придерживаются следующего алгоритма.
1) Найти первую производную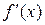 
.
2) Найти стационарные и критические точки функции и выбрать те из них, которые попадают в отрезок .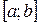
3) Сравнить значения функции в найденных точках и на границах (т.е. в точках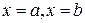 
), выбрать наибольшее и наименьшее значения. Характер экстремума определять не нужно.
Пусть функции 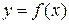определена в интервале 
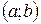. В этом случае не гарантируется существование наибольшего и наименьшего значений у функций. После определения стационарных и критических точек и значений функции в них, необходимо изучить поведение функции пр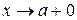и 
и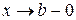 
. Сравнивая полученные значения, получают наибольшее или наименьшее значения функции или обосновывается факт отсутствия таких значений.
В случае бесконечных промежутков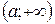 
, 
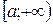и др. схема исследований аналогична. Наибольшее и наименьшее значения функции на числовом промежутке называют глобальными экстремумами функции.
