Краткие теоретические сведения. Функция называется первообразной для функции на некотором промежутке изменения переменной , если существует производная

Функция 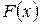называется первообразной для функции 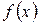на некотором промежутке изменения переменной 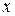, если существует производная 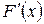при любых 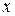из рассматриваемого промежутка и .

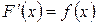Если функция 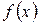имеет первообразную 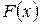, то она имеет бесконечное множество первообразных, причем все первообразные содержатся в выражении 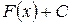, где 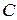- постоянная.

Неопределенным интегралом от функции 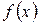называется совокупность всех ее первообразных.

Обозначени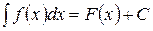е: , где 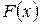– некоторая первообразная для 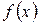, 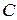– произвольная постоянная, 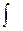– означает неопределенный интеграл, 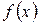называется подынтегральной функцией, 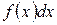– подынтегральным выражением, 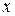– переменной интегрирования.

Процесс отыскания неопределенного интеграла от функции 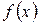называется интегрированием этой функции.

Простейшие свойства неопределенного интеграла:

1. Производная от неопределенного интеграла по переменной интегрирования равна подынтегральной функции: .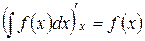

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению: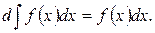

3. Неопределенный интеграл от производной от некоторой функции равен сумме этой функции и произвольной постоянной: .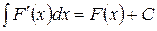

4. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:

.

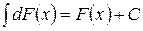5. Неопределенный интеграл от суммы функций равен сумме неопределенных интегралов от слагаемых:

.

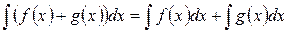6. Постоянный множитель можно выносить за знак неопределенного интеграла: .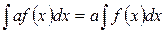

Таблица основных неопределенных интегралов

1.

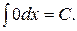
2.

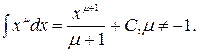
3.

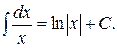
4. ,

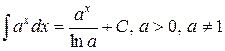в частности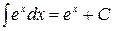

5.

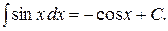
6.

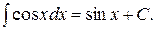
7.

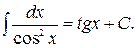
8.

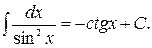
9.

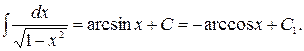
10.

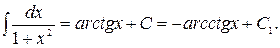
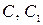– произвольные постоянные.