Пример 1. Вычислить площадь фигуры, ограниченной линиями 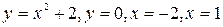
Решение. Построим чертёж
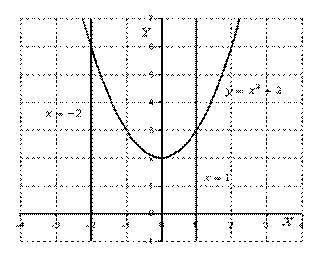
На отрезке 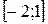 график функции
график функции 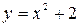 расположен над осью
расположен над осью 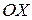 .
.
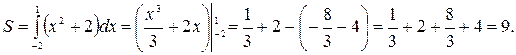
Ответ: 9 кв.ед.
Пример 2. Вычислить площадь фигуры, ограниченной линиями 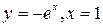 и координатными осями.
и координатными осями.
Решение. Выполним чертеж:
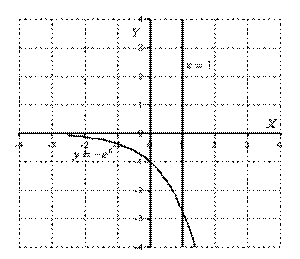
Криволинейная трапеция полностью расположена под осью 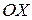 , её площадь можно найти по формуле:
, её площадь можно найти по формуле: 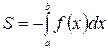 .
.
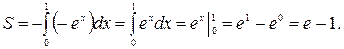
Ответ. 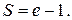
Пример 3. Найти площадь плоской фигуры, ограниченной линиями 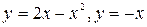 .
.
Решение. Выполним чертеж. Найдем точки пересечения параболы 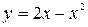 и прямой
и прямой 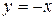 аналитически из уравнения:
аналитически из уравнения:
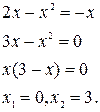
Значит, нижний предел интегрирования 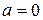 , верхний предел интегрирования
, верхний предел интегрирования 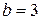 .
.
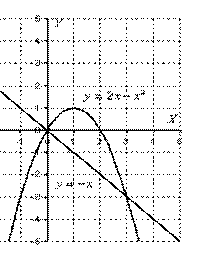
площадь соответствующей фигуры найдём по формуле:
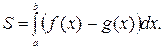
Искомая фигура ограничена параболой 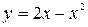 сверху и прямой
сверху и прямой 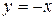 снизу.
снизу.
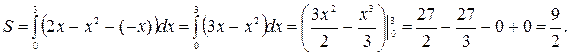
Ответ: S=4,5 кв.ед.
Пример 4. Вычислить объем тела, полученного вращением фигуры, ограниченной линиями 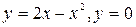 вокруг оси
вокруг оси 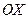 .
.
Решение. Выполним чертёж.
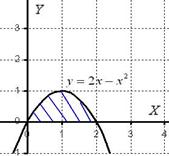
Вычислим объем тела вращения, используя формулу:
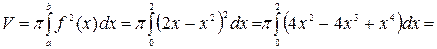
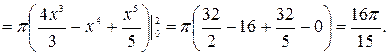
Ответ: 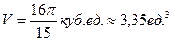
Пример 5. Дана плоская фигура, ограниченная линиями 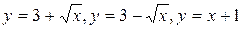 .
.
1) Найти площадь плоской фигуры, ограниченной данными линиями.
2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси 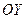 .
.
Решение. Выполним чертёж:

Площадь фигуры находится как сумма площадей:
– на отрезке 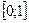
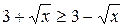 ;
;
– на отрезке 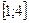
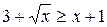 .
.
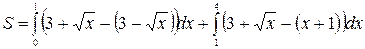
Есть более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси 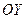 .
.
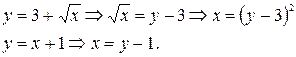
На отрезке 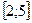
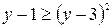 , поэтому:
, поэтому:
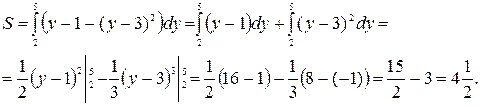
Вычислим объем тела, образованного вращением фигуры, вокруг оси 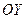 . Объем полученного тела вращения равен разности объемов
. Объем полученного тела вращения равен разности объемов 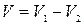 .
.
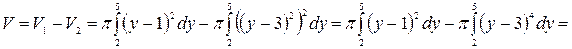
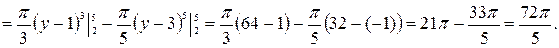
Ответ. 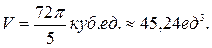
 2015-04-01
2015-04-01 4972
4972
