Предел и непрерывность функции комплексной переменной
Пусть задана функция комплексной переменной w = f (z)= u + iv, где z = x + iy, u (x, y) =Re w, v (x, y) =Im w.
Число А называется пределом функции f (z) при 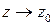 (
(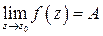 ), если
), если 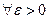
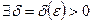 такое, что для всех z ≠ z 0, удовлетворяющих неравенству
такое, что для всех z ≠ z 0, удовлетворяющих неравенству 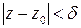 , выполняется неравенство
, выполняется неравенство 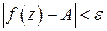 .
.
Функция f (z) называется непрерывной в точке 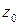 , если она определена в этой точке и выполняется равенство
, если она определена в этой точке и выполняется равенство 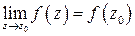 .
.
 2015-04-01
2015-04-01 439
439








