Обратным оператором Лапласа называется такой оператор L -1, который каждой функции 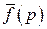 из класса лапласовых изображений непрерывных функций f (t), удовлетворяющих условиям Хевисайда, ставит в соответствие функцию f (t), т.е. если
из класса лапласовых изображений непрерывных функций f (t), удовлетворяющих условиям Хевисайда, ставит в соответствие функцию f (t), т.е. если 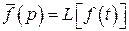 , то
, то 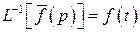 .
.
Переход от изображения к оригиналу называется обратным преобразованием Лапласа.
Заметим, что обратный оператор Лапласа L -1 обладает свойством линейности:
1) 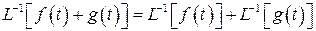
2) 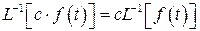
Малая таблицаобратных преобразований Лапласа
1) 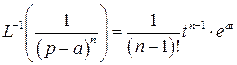
2) 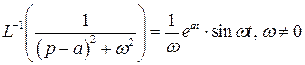
3) 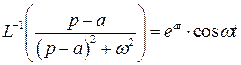
Обратное преобразование Лапласа дробно-рациональных функций
Нахождение обратного преобразования Лапласа любой правильной дробно-рациональной функции в силу линейности обратного преобразования Лапласа сводится к нахождению обратного преобразования Лапласа простейших дробно-рациональных функций.
Справедливы следующие формулы обратных преобразований Лапласа простейших дробно-рациональных функций:
1) 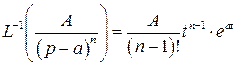 2)
2) 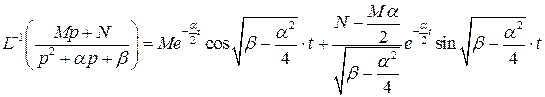
3) 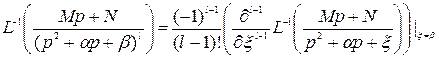
Здесь n =1,2,…; l =2,3,…; A, a, M, N, α, β - вещественные числа, 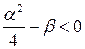 .
.
 2015-04-01
2015-04-01 1094
1094
