Оператором Лапласа называется такой оператор L, который каждой функции f (t)из рассматриваемого класса функций ставит в соответствие функцию
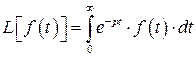 , (1)
, (1)
где p -параметр (может быть комплексным).
Если несобственный интеграл в правой части равенства (1) сходится при соответствующих значениях параметра p, то полагают
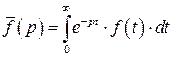 ,
,
при этом f (t) называется оригиналом, а функция 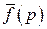 - его лапласовым изображением.
- его лапласовым изображением. 
Говорят, что функция f(t) удовлетворяет условиям Хевисайда, если:
1) f (t)=0 для любого t  < 0;
< 0;
2) существуют вещественные числа A >0 и k≥ 0 такие, что при 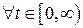 выполняется условие:
выполняется условие: 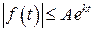 .
.
Теорема (о достаточном условии существования лапласового изображения). Для того чтобы существовало лапласово изображение функции f (t), достаточно, чтобы функция f (t) удовлетворяла условиям Хевисайда и выполнялось неравенство
Re p > k.
Заметим, что оператор Лапласа L обладает свойством линейности:
1) 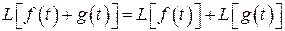
2) 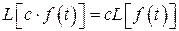
Малая таблица лапласовых изображений
1) 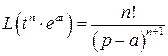
2) 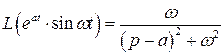
3) 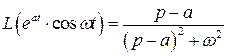
 Теорема (о лапласовом изображении производной от функции). Пусть функции
Теорема (о лапласовом изображении производной от функции). Пусть функции 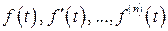 удовлетворяют условиям Хевисайда. Тогда справедлива формула:
удовлетворяют условиям Хевисайда. Тогда справедлива формула:
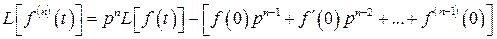 ,
,
(здесь 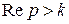 ).
).
 2015-04-01
2015-04-01 1161
1161
