Пусть функция w = f (z) задана в некоторой области D комплексной переменной z. Функция f (z) называется дифференцируемой в точке z, если существует конечный предел отношения приращения функции ∆ f (z) к приращению аргумента ∆ z при условии, что ∆ z →0. Этот предел называется производной функции  w = f (z) в точке z и обозначается
w = f (z) в точке z и обозначается 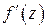 .Таким образом,
.Таким образом,
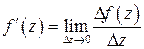 .
.
Теорема (критерий дифференцируемости функций комплексной переменной). Для того чтобы функция f (z)= u (x, y)+ iv (x, y) была дифференцируемой в точке z =x+iy, необходимо и достаточно, чтобы функции u (x, y) и v (x, y) были дифференцируемы в точке(x, y) как функции двух действительных переменных x, y и выполнялись условия Коши-Римана:
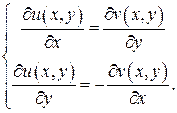 (1)
(1)
При выполнении условий (1) производная 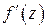 может быть записана в виде:
может быть записана в виде:
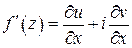 . (2)
. (2)
Заметим, что правила дифференцирования функции комплексной переменной аналогичны правилам дифференцирования функции действительной переменной.
Задание. Проверить выполнение условий Коши-Римана для функции f (z) и в случае их выполнения найти 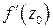 :
:
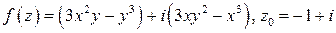 .
.
Решение. В данном случае
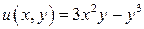 ,
,
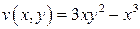 ,
,
и поэтому
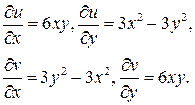
Следовательно, условия Коши-Римана выполняются во всей плоскости, и по формуле (2) имеем:
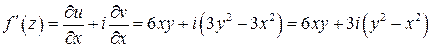 .
.
Тогда
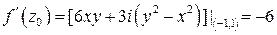 .
.
 2015-04-01
2015-04-01 3938
3938
