Пусть функция w = f (z) определена на дуге MN кривой L комплексной плоскости z. Разобьем дугу MN произвольным образом на n частей точками M=z 0, z 1,…, zn = N. Полученные дуги zi -1 zi, i= 1,…, n назовем элементарными дугами. В каждой из элементарных дуг произвольным образом выберем по точке 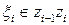 , i= 1,…, n, которые назовем точками пунктуации. Введем обозначения:
, i= 1,…, n, которые назовем точками пунктуации. Введем обозначения:
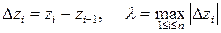
и составим сумму
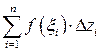 , (3)
, (3)
которая называется интегральной суммой Римана для функции f (z) по дуге MN. Заметим, что выражение (3) зависит от способа разбиения дуги MN на элементарные дуги и от способа выбора точек пунктуации.
Если существует предел интегральной суммы Римана (3) при 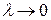 , и если этот предел не зависит ни от способа разбиения дуги MN на элементарные дуги, ни от выбора точек пунктуации, то он называется интегралом от функции комплексной переменной f (z) по дуге MN. При этом используется обозначение:
, и если этот предел не зависит ни от способа разбиения дуги MN на элементарные дуги, ни от выбора точек пунктуации, то он называется интегралом от функции комплексной переменной f (z) по дуге MN. При этом используется обозначение:
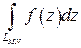 .
.
Таким образом, по определению

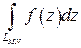 =
= 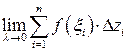 . (4)
. (4)
Если f (z)= u (x, y)+ iv (x, y), то интеграл представляется в виде суммы двух криволинейных интегралов 2-го рода:
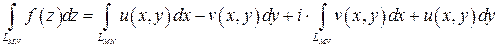 (5)
(5)
Задание. Вычислить интеграл 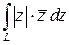 , где
, где 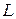 - верхняя полуокружность
- верхняя полуокружность 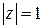 от точки
от точки 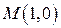 до точки
до точки 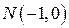 .
.
Решение. По формуле (5) имеем:
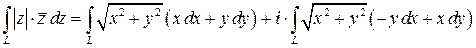 .
.
Переходя к параметрическому уравнению кривой 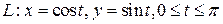 ,
,
получаем
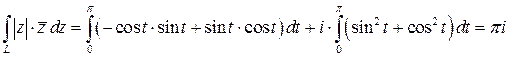 .
.
 2015-04-01
2015-04-01 879
879








