Фиктивные переменные. Тест Чоу

Факторы (объясняющие переменные), применяемые в задаче регрессии до сих пор, принимали значения из некоторого непрерывного интервала. Иногда может понадобиться ввести в модель переменные, значения которых детерминированы и дискретны. Например, данные получены для трех разных районов, или на двух фабриках, или на разных машинах и т.п. Переменные такого типа обычно называют фиктивными или искусственными. Эти переменные позволяют отразить в модели эффекты сдвига во времени или в пространстве, воздействия качественных переменных. Пример фиктивной переменной - это переменная 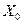при свободном члене 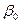в уравнении регрессии (3.1), которая принята равной 1. Эту переменную необязательно вводить в модель, но ее использование обеспечивает некоторое удобство в обозначениях. Во многих других случаях введение фиктивных переменных диктуется необходимостью.

Пример. Пусть, требуется отразить в модели разное происхождение куриных окороков (исходные данные - таблица 4.5), часть из которых получены в Америке, а часть в Канаде, при построении регрессионной зависимости веса окороков У от возраста кур Х. для этого в модель включим фиктивную переменную Z: Z=O для Америки, Z=1 для Канады:

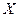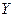	13,3	8,9	15,1	10,4	13,1	12,4	13,2	11,8	11,5	14,2	15,4

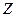Таблица 4.5 Данные для расчёта модели с фиктивными переменными

Построив регрессию 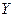по 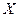приходим к уравнению

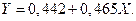
Используя модель с фиктивной переменной получим

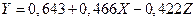
или для различных стран

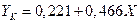для Канады и 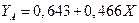для Америки.

Дисперсионный анализ показывает значимость полученных зависимостей, причем уравнение (как с фиктивной переменной, так и без фиктивной переменной) объясняет до 80% вариации относительно среднего.

Вывод: введение фиктивной переменной не дает весомого улучшения модели в смысле дополнительно объяснённой вариации.

Для любой задачи существует не единственный способ выбора фиктивных переменных. Это обстоятельство оказывается выгодным, поскольку в некоторых случаях можно угодить в ловушку, когда существует линейная зависимость между введенными фиктивными переменными.

Чтобы избежать ловушки, необходимо выбрать одну из категорий в качестве эталонной и определять фиктивные переменные для остальных возможных категорий, причем выбор эталонной категории не влияет на сущность регрессии.

Может потребоваться включение в модель более одной совокупности фиктивных переменных. Это особенно часто встречается при работе с перекрестными выборками.

Фиктивные переменные могут быть введены не только в правую часть регрессионного соотношения, но и зависимая переменная может быть представлена в такой форме. Это возможно в тех случаях, когда в качестве зависимой переменной рассматриваются ответы на вопросы, пользуется ли человек собственной машиной, имеет ли счет в банке и т.п., причем во всех случаях зависимая переменная принимает дискретные значения.

Фиктивные переменные могут быть использованы для учета взаимодействия между различными группами факторов.

Рассмотрим пример с окороками. Для построения двух прямых рассмотрим модель:

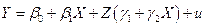или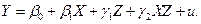

Такой подход позволяет проверить различные варианты гипотез:

1. Гипотеза 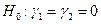против альтернативы 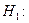что это не так. Если гипотеза 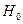будет отвергнута, то мы придем к выводу, что модели не одинаковы, а если нет, то можно пользоваться одной моделью независимо от происхождения окороков.

2. Если гипотеза 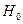в предыдущем пункте будет отвергнута, то можно проверить гипотезу 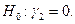Если 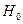принимается, то мы заключаем, что имеющиеся два набора данных отличаются только уровнем, имея одинаковые углы наклона.

При необходимости могут быть выбраны и другие варианты проверок, если это разумно для задачи. Получим для указанной выше модели уравнение МНК:

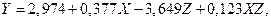
причём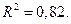

Два отдельных уравнения для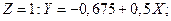

и для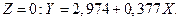

Для проверки гипотезы 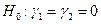составим таблицу дисперсионного анализа (табл. 4.6).

Источник вариации	Сумма квадратов	Степени свободы	Средний квадрат
Х Z,XZ Остаток Всего	24,447 6,797 6,881		10,414 3,399 0,983
38,125

Таблица 4.4

Значение 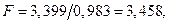что меньше 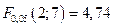и, следовательно, гипотеза принимается, т.е. можно пользоваться одной моделью как для окороков из Америки, так и из Канады. Последнее подтверждается ранее полученными результатами.

Часто эконометрист сталкивается с ситуацией, когда к уже имеющейся выборке он хочет присоединить небольшую дополнительную порцию данных, но не знает, можно ли считать выборки регрессионно-однородным.

Если необходимо выяснить, можно ли использовать одну и ту же модель для двух разных выборок данных или следует оценивать отдельные регрессии для каждой выборки, то можно воспользоваться тестом Чоv.

Рассмотрим модели:

;

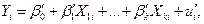
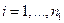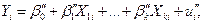
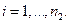
Требуется проверить гипотезу

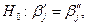
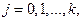
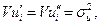
которая содержательно означает, что для двух имеющихся выборок из 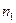и 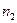наблюдений можно использовать одну и ту же регрессионную модель, т.е. выборки можно объединить.

Процедура Чоу для статистической проверки гипотезы 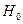состоит в следующем:

1. Строим МНК оценки регрессии (4.14) и вычисляем сумму квадратов остатков, которую обозначим через 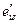.Строим МНК оценки регрессии (4.15) и вычисляем сумму квадратов остатков, которую обозначим через .

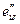2. Строим МНК оценки регрессии по объединенной (общей) выборке, содержащей в себе все наблюдения (числом 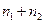)обеих выборок и вычисляем сумму квадратов остатков, которую обозначим через .

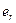3. Критическая статистика 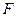вычисляется по формуле:

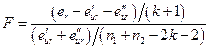
и имеет распределение Фишера с 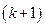и 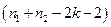степенями свободы. Если 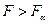, то нулевая гипотеза отвергается, и в этом случае мы не можем объединить две выборки в одну.