Стационарные временные ряды имеют следующие отличительные черты: значения ряда колеблются вокруг постоянного среднего значения с постоянной дисперсией, которая не зависит от времени, АКФ затухает с увеличением лага. При анализе экономических явлений чаще приходится иметь дело с нестационарными временными рядами, которые не имеют постоянного среднего, дисперсия которых зависит от времени, а АКФ затухает очень медленно. Для подбора модели ряда и прогнозирования его значений необходимо уметь. распознавать тип временного ряда.
Рассмотрим процесс авторегрессии первого порядка
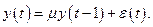
Ряд 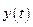 является стационарным рядом, если
является стационарным рядом, если 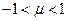 . Если
. Если 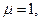 то
то 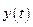
нестационарный временной ряд - случайное блуждание со сдвигом: в этом случае считают, что временной ряд 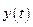 имеет единичный корень.
имеет единичный корень.
Вычтем 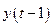 из обеих частей модели:
из обеих частей модели: 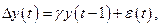 где
где 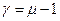 . Дики и Фуллер рассмотрели три регрессии:
. Дики и Фуллер рассмотрели три регрессии:
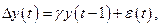
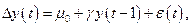
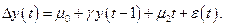
Вторая регрессия содержит постоянный элемент 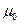 ,а третья, кроме этого, и линейный временной тренд. Во всех трех регрессиях интересующий параметр
,а третья, кроме этого, и линейный временной тренд. Во всех трех регрессиях интересующий параметр 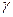 .
.
Нулевая гипотеза 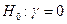 против альтернативы
против альтернативы 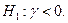
Тест Дики-Фуллера (Dickey-Fuller) состоит в следующем. Оцениваются методом наименьших квадратов одно из указанных выше уравнений.
Получают оценку 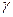 , стандартную ошибку и соответствующее значение (
, стандартную ошибку и соответствующее значение (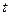 - статистики. Сравнивая значение (
- статистики. Сравнивая значение (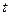 - статистики с табличным, определяют, принять или отклонить
- статистики с табличным, определяют, принять или отклонить 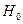 . Критическое значение (
. Критическое значение (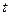 -статистики имеет нестандартное распределение и зависит от формы регрессии и объема выборки.
-статистики имеет нестандартное распределение и зависит от формы регрессии и объема выборки.
Критические значения не изменятся, если указанные выше модели заменить авторегрессионным процессом произвольного порядка:
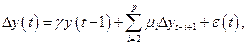
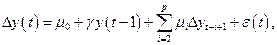
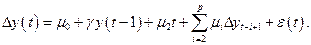
Для последних моделей Дики и Фуллер предложили три дополнительные статистики для тестирования обобщенных гипотез о коэффициентах:
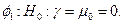
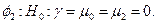
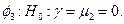
Статистики 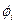 констатируются как
констатируются как 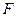 тест
тест 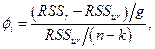
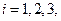 где
где 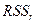 и
и 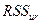 - квадраты ошибок короткой и длинной регрессий,
- квадраты ошибок короткой и длинной регрессий, 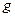 - число исключенных переменных,
- число исключенных переменных, 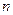 - число наблюдений,
- число наблюдений, 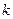 - число параметров в длинной регрессии. Большие значения
- число параметров в длинной регрессии. Большие значения 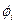 ведут к отклонению нулевой гипотезы. Критические значения статистик вычислены Дики и Фуллером и затабулированы.
ведут к отклонению нулевой гипотезы. Критические значения статистик вычислены Дики и Фуллером и затабулированы.
 2015-04-01
2015-04-01 375
375








