Решение

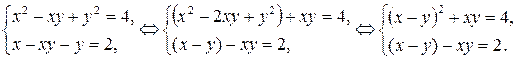
Сделаем замену: 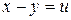, , 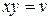тогда

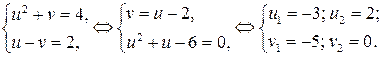
Переходя к исходным переменным, получим:

1) 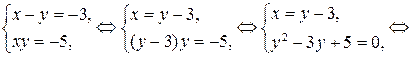решений нет.

2)

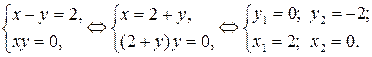
Ответ: .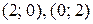

Пример 9.5. Решить систему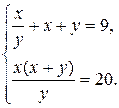

Решение. Сделаем замену: 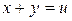, , 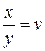тогда

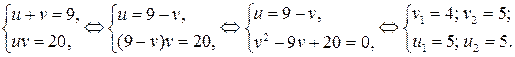
Переходя к исходным переменным, получим:

1)

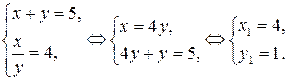
2)

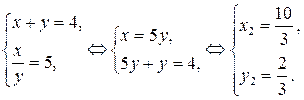
Ответ: .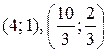

Пример 9.6. Решить систему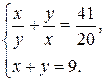

Решение. Первое уравнение является однородным относительно 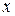и 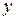. Сделаем замену: 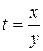, тогда

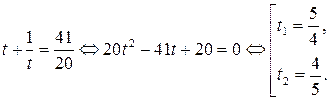
Переходя обратно к переменным , :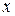

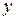1)

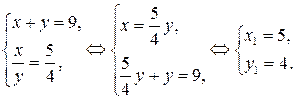
2)

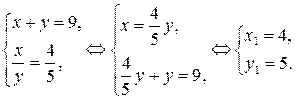
Ответ: .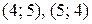

Пример 9.7. Решить систему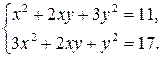

Решение. Умножим первое уравнение системы на 17, а второе – на 11:

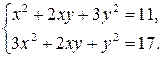
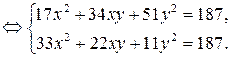
Вычтем из первого уравнения второе:

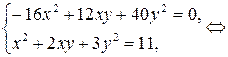
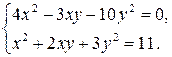
Первое уравнение является однородным. Учитывая, что 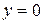не является решением системы, разделим его на :

.

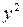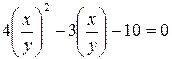Сделаем замену: 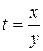, тогда

.

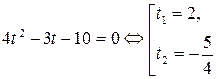Возвращаясь к исходным переменным, в итоге имеем:

1)

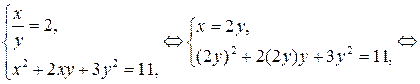
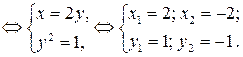
2)

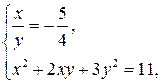
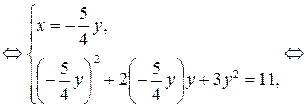
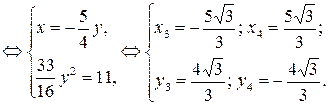
Ответ: .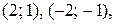

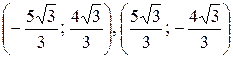Пример 9.8. Решить систему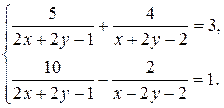

Решение. Сделаем замену: 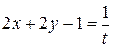, , 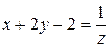тогда исходная система примет вид 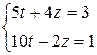. Умножим второе уравнение на 2 и прибавим его к первому:

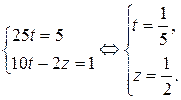
Переходя обратно к переменным 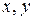, имеем:

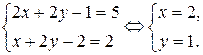
Ответ: .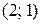

Пример 9.9. Решить систему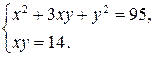

Решение. Многочлены в правых частях уравнения системы являются симметричными относительно неизвестных 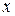и 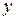. Проведем следующие преобразования:

.

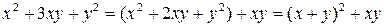Сделаем замену: 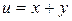, , 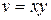тогда исходная система примет вид:

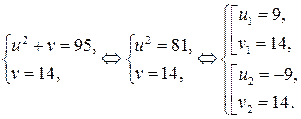
Возвращаясь к исходным переменным, имеем

1) 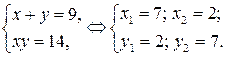2)

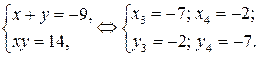
Ответ: .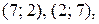

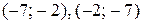Пример 9.10. Решить систему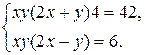

Решение. Разделим первое уравнение системы на второе:

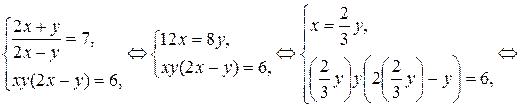
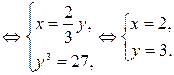
Ответ: .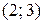

Замечание 9.2. Рассмотренные в данном пункте методы также используют для решения систем, где функци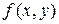и и 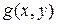не являются многочленами. В этом случае необходимо следить за областью определения и стараться избегать переходов, при которых могут появиться посторонние решения или возможна потеря решений.