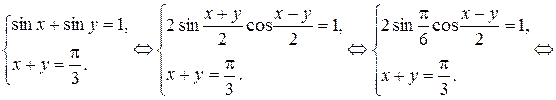
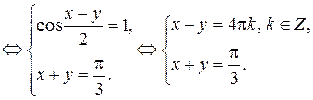
Сложим и вычтем уравнения системы:
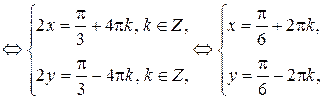
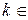
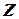 .
.
Ответ: 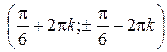 ,
, 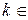
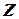 .
.
Пример 9.23. Решить систему 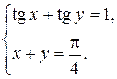
Решение. Преобразуем первое уравнение системы:
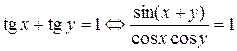 ,
,
тогда
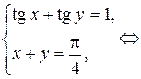
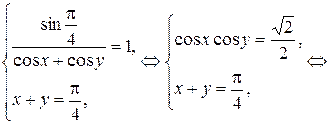
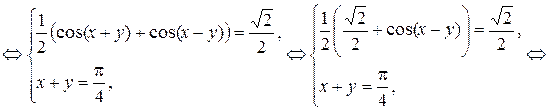
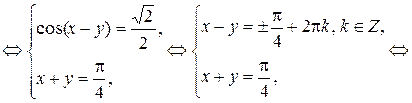
1) 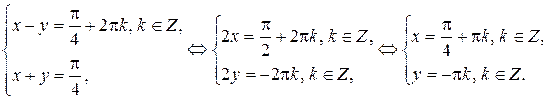
2) 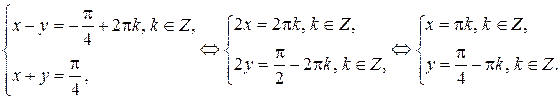
Ответ: 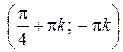 ,
, 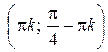 ,
, 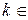
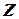 .
.
Пример 9.24. Решить систему 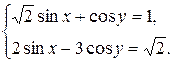
Решение. Сделаем замену: 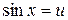 ,
, 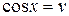 ,
, 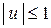 ,
, 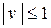 , тогда исходная система примет вид:
, тогда исходная система примет вид: 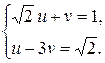 Умножим первое уравнение системы на 3 и прибавим ко второму:
Умножим первое уравнение системы на 3 и прибавим ко второму:
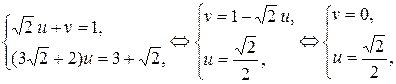
возвращаясь к исходным переменным, имеем
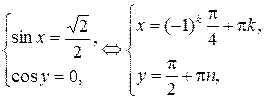
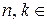
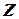 .
.
Ответ: 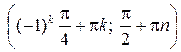 ,
, 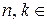
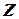 .
.
Пример 9.25. Решить систему 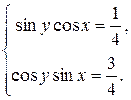
Решение. Сложим и вычтем уравнения системы, тогда
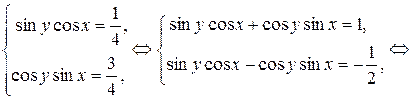
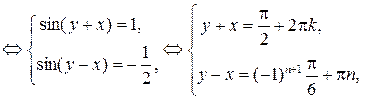
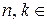
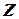
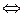 .
.
1) 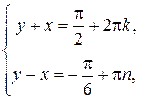
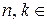
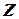
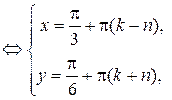
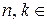
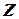 ,
,
2) 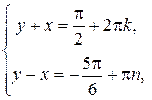
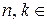
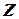
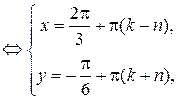
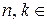
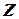 .
.
Ответ: 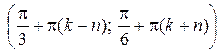 ;
; 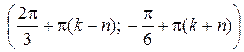 ,
, 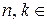
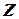 .
.
Пример 9.26. Решить систему 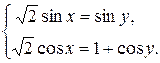
Решение. Возведем обе части уравнений системы в квадрат и сложим их:
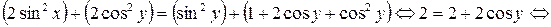
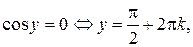
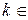
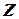 .
.
Подставим полученное выражение для неизвестной 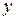 в исходную систему, тогда получаем:
в исходную систему, тогда получаем:
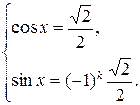
Возможны следующие случаи.
1) Если 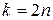 ,
, 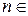
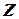 , то, учитывая, что
, то, учитывая, что 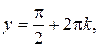
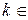
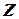 , имеем
, имеем
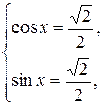 откуда
откуда 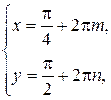
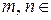
 .
.
2) Аналогично, если 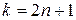 ,
, 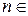
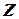 , то,
, то,
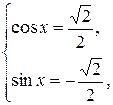 откуда
откуда 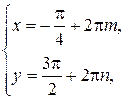
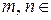
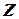 .
.
Ответ: 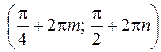 ;
; 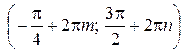 ,
, 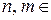
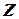 .
.
 2015-04-01
2015-04-01 939
939








