Пример 9.16. Решить систему 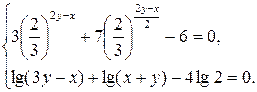
Решение. Область определения системы описывается условиями:
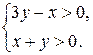
Сделаем в первом уравнении системы замену 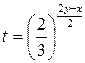 ,
, 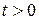 , тогда получим
, тогда получим
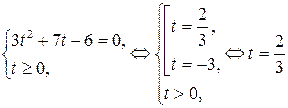 ,
,
или, переходя к исходным переменным,
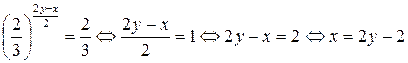 .
.
Подставим полученное выражение для неизвестной 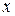 во второе уравнение системы:
во второе уравнение системы:
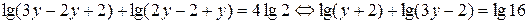 ,
,
откуда
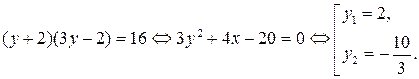
Соответствующие 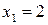 ;
; 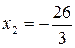 . Проверкой убеждаемся, что пара
. Проверкой убеждаемся, что пара 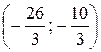 не входит в область определения системы, то есть является посторонним решением.
не входит в область определения системы, то есть является посторонним решением.
Ответ: 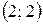 .
.
Пример 9.17. Решить систему 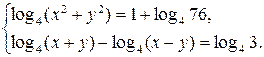
Решение. Область определения системы: 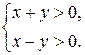
Используя свойства логарифмов, преобразуем исходную систему:
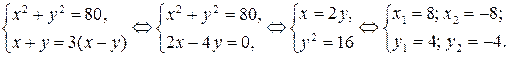
Делая проверку, получаем, что 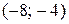 - постороннее решение.
- постороннее решение.
Ответ: 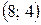 .
.
Пример 9.18. Решить систему 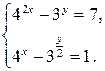
Решение. 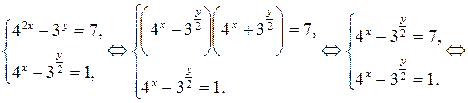
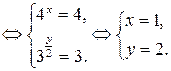
Ответ: 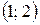 .
.
Пример 9.19. Решить систему 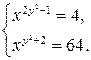
Решение. Область определения системы 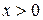 ,
, 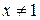 . Прологарифмируем первое и второе уравнения системы по основанию
. Прологарифмируем первое и второе уравнения системы по основанию 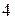 и проведем преобразования системы на ОДЗ:
и проведем преобразования системы на ОДЗ:
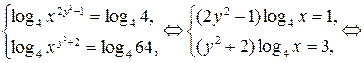
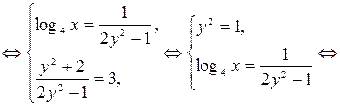
1) 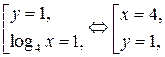 2)
2) 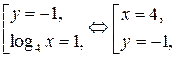
Ответ: 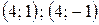 .
.
Пример 9.20. Решить систему 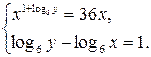
Решение. Область определения системы 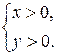 . Преобразуем исходную систему:
. Преобразуем исходную систему: 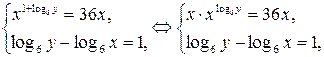 откуда, учитывая, что
откуда, учитывая, что 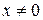 ,
,
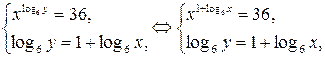
прологарифмируем первое уравнение системы по основанию 6 и потенцируем второе, тогда
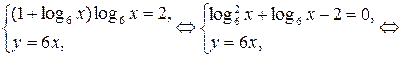
1) 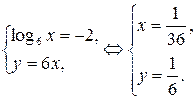 2)
2) 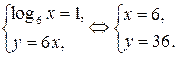
Ответ: 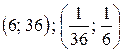 .
.
Пример 9.21. Решить систему 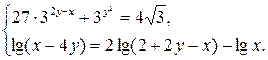
Решение. Область определения системы 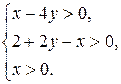 Проведем преобразования системы на ОДЗ:
Проведем преобразования системы на ОДЗ:
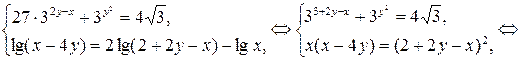
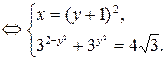
Рассмотрим второе уравнение системы. Введем замену: 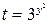 ,
, 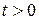 , тогда
, тогда
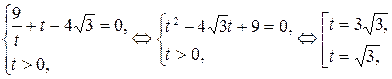
делая обратную замену, имеем
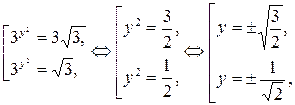 ,
,
или в итоге 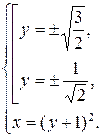 . Так как
. Так как 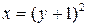 , преобразуем выражения для области определения системы
, преобразуем выражения для области определения системы
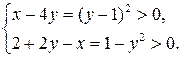
Следовательно, решениями являются 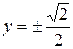 и
и 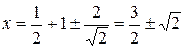 .
.
Ответ: 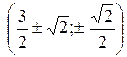 .
.
 2015-04-01
2015-04-01 4709
4709
