1. Найти производную функции.
2. Найти критические точки функции и выбрать те, которые принадлежат данному отрезку.
3. Вычислить значения функции в критических точках и на концах отрезка.
4. Из вычисленных значений выбрать наименьшее и наибольшее.
Пример 10.11. Найти точку максимума функции 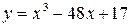 .
.
Решение. 1. 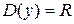
2. Найдем производную функции: 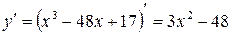 .
.
3. Критические точки:
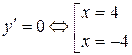 .
.
Производная существует во всех точках области определения функции.
4. Отметим найденные точки на числовой оси и определим знак производной справа и слева от этих точек:
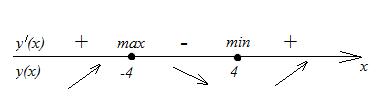
|
При переходе через точку 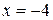 знак производной меняет свой знак с плюса на минус, следовательно, в силу теоремы 10.4,
знак производной меняет свой знак с плюса на минус, следовательно, в силу теоремы 10.4, 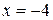 - точка максимума.
- точка максимума.
Ответ: 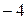 .
.
Пример 10.12. Найти наименьшее значение функции 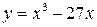 на отрезке
на отрезке 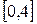 .
.
Решение. Воспользуемся схемой нахождения наибольшего и наименьшего значения функции на отрезке, представленной выше.
1. Найдем производную функции: 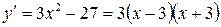 .
.
2. Критические точки:
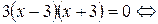
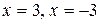 .
.
Отрезку 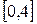 принадлежит только точка
принадлежит только точка 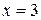 .
.
3. Вычислим значения функции в критической точке и на концах отрезка:
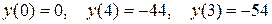 .
.
4. Наименьшее значение 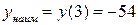 .
.
Ответ: 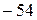 .
.
 2015-04-01
2015-04-01 532
532








