Комплексное число 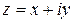 можно изобразить на координатной плоскости
можно изобразить на координатной плоскости 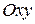 (комплексной области) точкой с координатами
(комплексной области) точкой с координатами 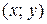 , либо радиус-вектором
, либо радиус-вектором 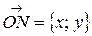 (рис. 11.1).
(рис. 11.1).
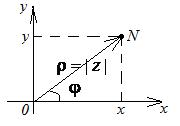 | Определение 11.5. Длина вектора 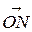 называется модулем комплексного числа: называется модулем комплексного числа: 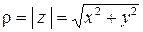 . Определение 11.6. Угол . Определение 11.6. Угол 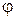 , образованный вектором , образованный вектором 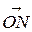 и осью и осью 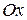 называется аргументом комплексного называется аргументом комплексного |
| рис. 11.1. |
числа. Обозначают 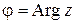 , причем
, причем
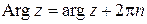 ,
, 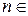
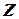 .
.
Здесь 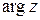 - главное значение аргумента.
- главное значение аргумента.
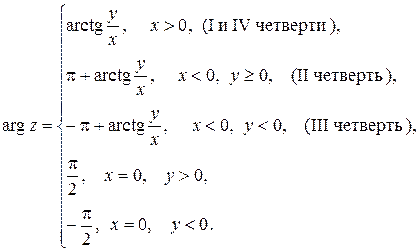
Замечание 11.2. Из рис. 12.1 видно, что справедливы следующие равенства: 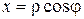 ,
, 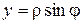 .
.
Учитывая замечание 12.2, можно сформулировать следующее определение.
Определение 11.7. Тригонометрической формой комплексного числа называется запись вида
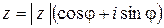
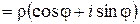 .
.
С помощью тригонометрической формы удобно находить произведение и частное комплексных чисел.
Пусть 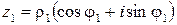 ,
, 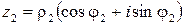 , тогда
, тогда
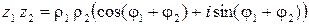 ,
,
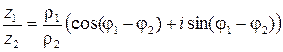 .
.
Возведение комплексного числа 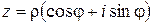 в натуральную степень
в натуральную степень 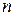 находится по формуле
находится по формуле
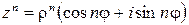 . . | (11.1) |
Корень 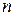 -ой степени из комплексного числа имеет
-ой степени из комплексного числа имеет 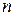 различных значений, которые выражаются формулой
различных значений, которые выражаются формулой
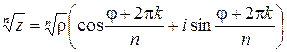 , где , где 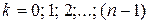 . . | (11.2) |
Замечание 11.1. Точки, соответствующие значениям 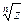 , являются вершинами правильного
, являются вершинами правильного 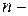 угольника, вписанного в окружность радиуса
угольника, вписанного в окружность радиуса 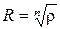 с центром в начале координат.
с центром в начале координат.
Формулы (11.1) и (11.2) называются формулами Муавра-Лапласа.
Определение 11.8. Показательной формой комплексного числа называется запись вида
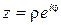 .
.
Пример 11.2. Записать комплексное число 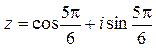 в алгебраической форме.
в алгебраической форме.
Решение. 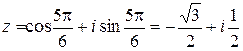 .
.
Пример 11.3. Записать в тригонометрической форме комплексные числа:
1) 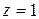 ; 2)
; 2) 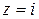 ; 3)
; 3) 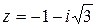 .
.
Решение. 1) 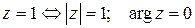 , откуда
, откуда 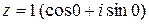 .
.
2) 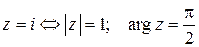 , откуда
, откуда 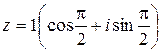 .
.
3) 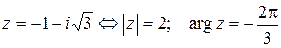 , откуда
, откуда 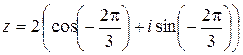 .
.
Пример 11.4. Вычислить 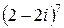 .
.
Решение. Представим комплексное число 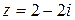 в тригонометрической форме:
в тригонометрической форме: 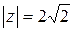 ,
, 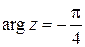 , следовательно,
, следовательно,
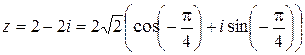 .
.
Тогда в силу формулы (11.1) имеем
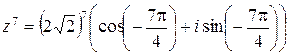
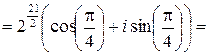
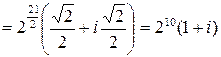 .
.
Пример 11.5. Найти все значения корня: 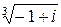 .
.
Решение. Представим комплексное число 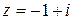 в тригонометрической форме:
в тригонометрической форме: 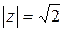 ,
, 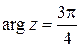 , следовательно,
, следовательно,
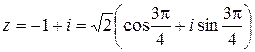 .
.
Тогда в силу формулы (11.2) получаем
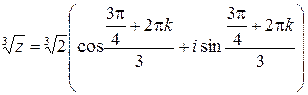 , где
, где 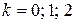 .
.
При 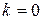 :
: 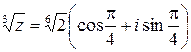
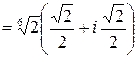 .
.
При 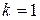 :
: 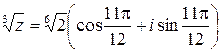 .
.
При 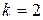 :
: 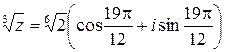 .
.
 2015-04-01
2015-04-01 929
929








