Пусть 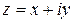 ,
, 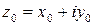 . Заметим, что неравенство
. Заметим, что неравенство 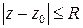 , или, что тоже самое,
, или, что тоже самое, 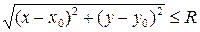
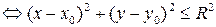 , задает круг с центром в точке
, задает круг с центром в точке 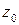 радиуса
радиуса 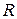 . Неравенство
. Неравенство 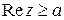 задает полуплоскость, расположенную правее прямой
задает полуплоскость, расположенную правее прямой 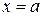 , а неравенство
, а неравенство 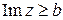 - полуплоскость, расположенную выше прямой
- полуплоскость, расположенную выше прямой 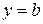 . Кроме того, система неравенств
. Кроме того, система неравенств 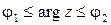 задает угол между лучами
задает угол между лучами 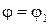 и
и 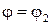 , выходящими из начала координат.
, выходящими из начала координат.
Пример 11.6. Нарисовать множество точек плоскости комплексного переменного 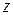 , которые определяются заданными условиями:
, которые определяются заданными условиями:
1) 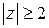 ; 2)
; 2) 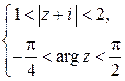 ; 3)
; 3) 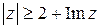 ; 4)
; 4) 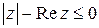 .
.
Решение. 1) 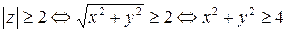 (рис. 12.2).
(рис. 12.2).
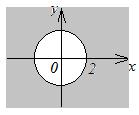 | 2) Первому неравенству соответствует кольцо с центром в точке 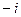 и двумя радиусами 1 и 2, окружности в область не входят (рис. 12.3). Второму неравенству соответствует угол между лучами и двумя радиусами 1 и 2, окружности в область не входят (рис. 12.3). Второму неравенству соответствует угол между лучами 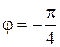 (биссектриса 4 координатного угла) и (биссектриса 4 координатного угла) и |
| рис. 11.2. |
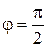 (положительное направление оси
(положительное направление оси 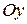 ). Сами лучи в область не входят (рис. 11.4). Искомая область является пересечением двух полученных областей (рис. 11.5).
). Сами лучи в область не входят (рис. 11.4). Искомая область является пересечением двух полученных областей (рис. 11.5).
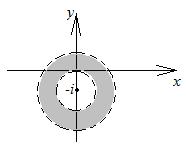 | 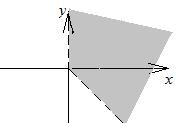 | 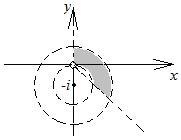 |
| рис. 11.3. | рис. 11.4. | рис. 11.5. |
3) 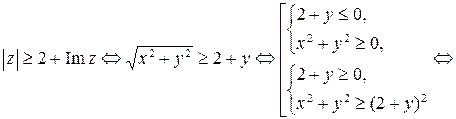
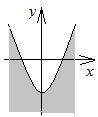
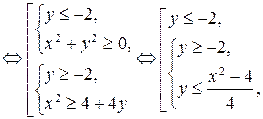 (рис. 11.6).
(рис. 11.6).
 | 4) 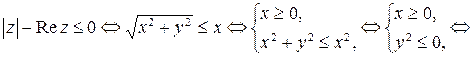 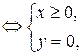 - действительная полуось, включая точку - действительная полуось, включая точку 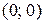 . Пример 11.7.Написать в комплексной форме уравнение окружности . Пример 11.7.Написать в комплексной форме уравнение окружности 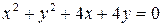 . . |
| рис. 11.6. |
Решение. Так как 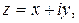
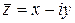 , то справедливы следующие выражения
, то справедливы следующие выражения 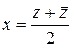 ,
, 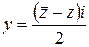 и
и 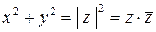 . Подставляя в уравнение окружности, получаем
. Подставляя в уравнение окружности, получаем
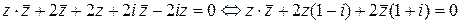 .
.
 2015-04-01
2015-04-01 7339
7339








